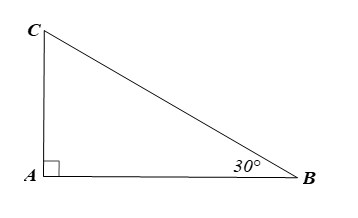
Cho tam giác ABC vuông tại A có góc B= 30 độ. Chứng minh AC = 1/2 BC
Câu hỏi:
Cho tam giác ABC vuông tại A có Chứng minh
Trả lời:
Xét ∆ABC vuông tại A, ta có:
Vậy
Câu hỏi:
Cho tam giác ABC vuông tại A có Chứng minh
Trả lời:

Xét ∆ABC vuông tại A, ta có:
Vậy
Câu 1:
Hình 12 mô tả đường lên dốc ở Hình 11, trong đó góc giữa BC và phương nằm giữa BA là

Cạnh góc vuông AC và cạnh huyền BC (Hình 12) có liên hệ với nhau như thế nào?
Câu 6:
Trong Hình 24, cho và
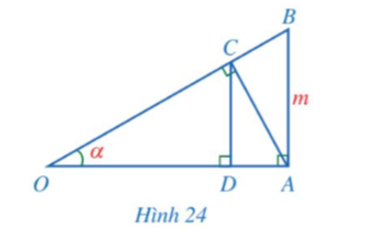
Chứng minh:
a) OA = m.cotα;
b) AC = m.cosα;
c) CD = m.cos2α.
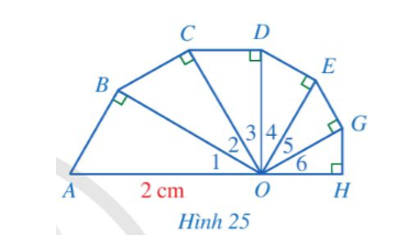
Câu 7:
Tính độ dài đường gấp khúc ABCDEGH (làm tròn kết quả đến hàng phần mười của centimét), biết các tam giác OAB, OBC, OCD, ODE, OEG, OGH là các tam giác vuông tại các đỉnh lần lượt là B, C, D, E, G, H; các góc O1, O2, O3, O4, O5, O6 đều bằng 30° và OA = 2 cm (Hình 25).
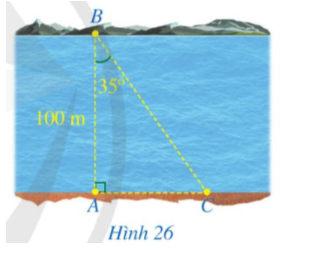
Câu 8:
Hình 26 minh hoạ một phần con sông có bề rộng AB = 100 m. Một chiếc thuyền đi thẳng từ vị trí B bên này bờ sông đến vị trí C bên kia bờ sông. Tính quãng đường BC (làm tròn kết quả đến hàng phần mười của mét), biết