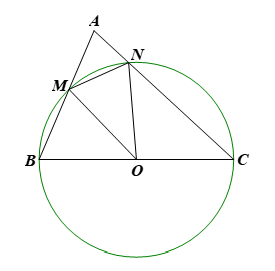
Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh MN < BC.
Câu hỏi:
Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh MN < BC.
Trả lời:
Nối OM, ON.
Xét ∆OMN, ta có: MN < OM + ON (Bất đẳng thức tam giác). (1)
Vì B, M, N, C cùng thuộc đường tròn (O) nên OA = OM = ON = OB.
Ta có: OM + ON = OB + OC.
Lại có BC là đường kính của đường tròn (O) nên BC = OB + OC.
Do đó OM + ON < BC. (2)
Từ (1) và (2) suy ra MN < AB.
Xem thêm lời giải bài tập Toán 9 Cánh diều hay, chi tiết:
Câu 1:
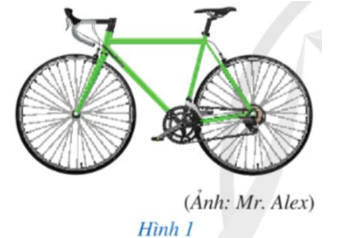
Mỗi bánh xe đạp ở Hình 1 gợi nên hình ảnh của một đường tròn.
Hai đường tròn đó có điểm chung hay không?
Xem lời giải »
Câu 2:
Đồng hồ được mô tả ở Hình 2 có kim phút dài 12 cm. Khi kim phút quay một vòng thì đầu mút của kim phút vạch nên đường gì?
Xem lời giải »
Câu 3:
Hãy chỉ ra một số đồ vật trong thực tiễn gợi nên hình ảnh của đường tròn.
Xem lời giải »
Câu 4:
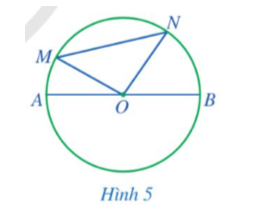
Quan sát Hình 5.
a) So sánh MN và OM + ON.
b) So sánh MN và AB.
Xem lời giải »
Câu 5:
Cho đường tròn (O; R).
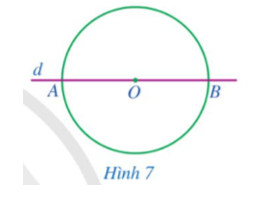
a) Vẽ đường thẳng d đi qua tâm O cắt đường tròn tại A, B. So sánh OA và OB (Hình 7).
b) Giả sử M là một điểm tùy ý trên đường tròn (O; R). Trên tia đối của tia OM, ta lấy điểm N sao cho ON = OM. Điểm N có thuộc đường tròn (O; R) hay không?
Xem lời giải »
Câu 6:
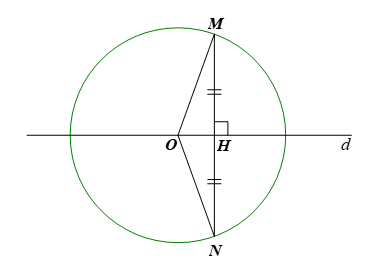
Cho đường tròn (O; R). Giả sử d là đường thẳng đi qua tâm O, M là một điểm tùy ý trên đường tròn (O; R). Kẻ MH vuông góc với d tại H. Trên tia MH lấy điểm N sao cho H là trung điểm của MN (ta gọi điểm N là điểm đối xứng với điểm M qua đường thẳng d). Điểm N có thuộc đường tròn (O; R) hay không?
Xem lời giải »
Câu 7:
Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm của hình đó.
Xem lời giải »
Câu 8:
Bạn Đan vẽ năm vòng tròn minh họa cho biểu tượng của Thế vận hội Olympic như ở Hình 10. Hình vẽ đó thể hiện những cặp đường tròn cắt nhau. Theo em, hai đường tròn cắt nhau thì chúng có bao nhiêu điểm chung?
Xem lời giải »