Tổng hợp lý thuyết Toán 9 Chương 3 - Cánh diều

---

Tổng hợp lý thuyết Toán 9 Chương 3: Căn thức sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm Toán 9 Chương 3.

Tổng hợp lý thuyết Toán 9 Chương 3 - Cánh diều

Lý thuyết tổng hợp Chương 3

1. Căn bậc hai của số thực không âm

Khái niệm: Căn bậc hai của một số thực a không âm là số thực x sao cho x² = a.

Chú ý:

⦁Khi a > 0, số a có đúng hai căn bậc hai là hai số đối nhau: số dương kí hiệu là $\sqrt{a}$ số âm kí hiệu là $-\sqrt{a}$. Ta gọi là căn bậc hai số học của a.

⦁ Căn bậc hai của số 0 bằng 0, kí hiệu là $\sqrt{0}$

⦁Số âm không có căn bậc hai.

Lưu ý:

⦁ Với a ≥ 0, ta có: ${\left(\sqrt{a}\right)}^2=a.$

⦁Với hai số a, b không âm, ta có:

Nếu a < b thì $\sqrt{a}<\sqrt{b};$

Nếu $\sqrt{a}<\sqrt{b}$ thì a < b.

2. Căn bậc ba

Khái niệm: Căn bậc ba của một số thực a là số thực x sao cho x³ = a.

Căn bậc ba của số thực a được kí hiệu là $\sqrt[3]{a}.$

Chú ý: Người ta chứng minh được rằng: Mỗi số thực a đều có duy nhất một căn bậc ba.

Lưu ý:

⦁Với mọi số thực a, ta có ${\left(\sqrt[3]{a}\right)}^3=a.$

⦁Với hai số a, b, ta có:

Nếu a < b thì $\sqrt[3]{a}<\sqrt[3]{b};$

Nếu $\sqrt[3]{a}<\sqrt[3]{b}$ thì a < b.

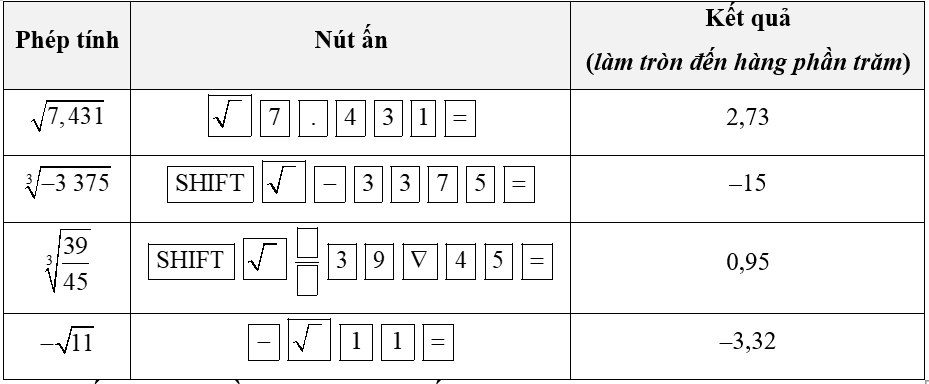
3. Sử dụng máy tính cầm tay để tìm căn bậc hai, căn bậc ba của một số hữu tỉ

⦁ Để tính căn bậc hai của một số hữu tỉ dương, ta sử dụng phím $\boxed{\sqrt{}}$

⦁ Để tính căn bậc ba của một số hữu tỉ, ta sử dụng liên tiếp hai phím $\boxed{SHIFT}\boxed{\sqrt{}}.$

Ví dụ:Sử dụng máy tính cầm tay để tính giá trị (đúng hoặc gần đúng, kết quả làm tròn đến hàng phần trăm) của:

a) $\sqrt{7,431};$

b) $\sqrt[3]{-3375};$

c) $\sqrt[3]{\frac{39}{45}};$

d) $-\sqrt{11}.$

Hướng dẫn giải

Ta sử dụng máy tính cầm tay như sau:

4. Một số phép tính về căn bậc hai của số thực

4.1. Căn bậc hai của một bình phương

Quy tắc: Với mọi số a, ta có $\sqrt{a^2}=\left|a\right|.$

Quy tắc: Với hai số không âm a và b, ta có $\sqrt{a\cdot b}=\sqrt{a}\cdot \sqrt{b}.$

Chú ý: Quy tắc trên có thể mở rộng cho tích có nhiều thừa số không âm.

4.3. Căn bậc hai của một thương

Quy tắc: Với a ≥ 0 và b > 0, ta có $\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}.$

4.4. Đưa thừa số ra ngoài dấu căn bậc hai

Quy tắc: Cho hai số a, b với b ≥ 0. Khi đó $\sqrt{a^2\cdot b}=\left|a\right|\sqrt{b}.$

Cụ thể, ta có:

Nếu a ≥ 0 và b ≥ 0 thì $\sqrt{a^{2}b}=a\sqrt{b};$

Nếu a < 0 và b ≥ 0 thì $\sqrt{a^{2}b}=-a\sqrt{b}.$

4.5. Đưa thừa số vào trong dấu căn bậc hai

Quy tắc: Với a ≥ 0 và b ≥ 0 thì $a\sqrt{b}=\sqrt{a^{2}b};$

Nếu a < 0 và b ≥ 0 thì $a\sqrt{b}=-\sqrt{a^{2}b}.$

5. Căn thức bậc hai

– Khái niệm: Với A là một biểu thức đại số, người ta gọi $\sqrt{A}$ là căn thức bậc hai của A, còn A được gọi là biểu thức lấy căn bậc hai hay biểu thức dưới dấu căn.

– Điều kiện xác định cho căn thức bậc hai $\sqrt{A}$ là A ≥ 0.

6. Căn thức bậc ba

– Khái niệm: Với A là một biểu thức đại số, người ta gọi là căn thức bậc ba của A, còn A được gọi là biểu thức lấy căn bậc ba hay biểu thức dưới dấu căn.

Chú ý: Các số, biến số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, khai căn (bậc hai hoặc bậc ba) làm thành một biểu thức đại số.

– Điều kiện xác định cho căn thức bậc ba $\sqrt[3]{A}$ chính là điều kiện xác định của biểu thức A.

7. Một số phép biến đổi căn thức bậc hai của biểu thức đại số

7.1. Căn thức bậc hai của một bình phương

Quy tắc: Với mỗi biểu thức A, ta có $\sqrt{A^2}=\left|A\right|,$ tức là: 

$\sqrt{A^2}=\left|A\right|=A$ nếu A ≥ 0;

$\sqrt{A^2}=\left|A\right|=-A$ nếu A < 0.

7.2. Căn thức bậc hai của một tích

Quy tắc: Với các biểu thức A, B không âm, ta có $\sqrt{A\cdot B}=\sqrt{A}\cdot \sqrt{B}.$

7.3. Căn thức bậc hai của một thương

Quy tắc: Với biểu thức A không âm và biểu thức B dương, ta có $\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}.$

7.4. Trục căn thức ở mẫu

Phép biến đổi làm mất căn thức ở mẫu thức của một biểu thức được gọi là trục căn thức ở mẫu của biểu thức đó.

Chú ý

⦁Các biểu thức A, B mà B > 0, ta có: $\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}.$

⦁Các biểu thức A, B, C mà B ≥ 0 và A² ≠ B, ta có:

$\frac{C}{A+\sqrt{B}}=\frac{C\left(A-\sqrt{B}\right)}{A^2-B};\frac{C}{A-\sqrt{B}}=\frac{C\left(A+\sqrt{B}\right)}{A^2-B}.$

Biểu thức $A-\sqrt{B}$ được gọi là biểu thức liên hợp của $A+\sqrt{B}$ và ngược lại.

⦁Các biểu thức A, B, C mà A ≥ 0, B ≥ 0 và A ≠ B, ta có:

$\frac{C}{\sqrt{A}+\sqrt{B}}=\frac{C\left(\sqrt{A}-\sqrt{B}\right)}{A-B};\frac{C}{\sqrt{A}-\sqrt{B}}=\frac{C\left(\sqrt{A}+\sqrt{B}\right)}{A-B}.$

Biểu thức $\sqrt{A}-\sqrt{B}$ được gọi là biểu thức liên hợp của $\sqrt{A}+\sqrt{B}$ và ngược lại.

Bài tập ôn tập Chương 3

I. Bài tập trắc nghiệm

Bài 1. Số nào sau đây là căn bậc hai của 100?

A. 10;

B. –10;

C. 50;

D. –10 và 10.

Hướng dẫn giải

Đáp án đúng là: D

Ta có: 10² = 100 và (–10)² = 100 nên số 10 và –10 là căn bậc hai của 100.

Bài 2. Số 25 là căn bậc hai của số nào sau đây?

A. 5;

B. 12,5;

C. 625;

D. Một đáp án khác.

Hướng dẫn giải

Đáp án đúng là: C

Ta có 25² = 625 nên 25 là căn bậc hai của số 625.

Bài 3.Khẳng định nào sau đây đúng?

A. $\sqrt[3]{a}=x$ nếu a³ = x;

B. $\sqrt[3]{a}=-x$ nếu a³ = x;

C. $\sqrt[3]{a}=x$ nếu a = x³;

D. $\sqrt[3]{a}=-x$ nếu a = x³.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: $\sqrt[3]{a}=x$ nếu a = x³.

Bài 4.Biểu thức $\sqrt[3]{16\text{x}-5}$ có nghĩa khi

A. $x\ne \frac{5}{16};$

B. $x\ge \frac{5}{16};$

C. $x\le \frac{5}{16};$

D. x là số thực.

Hướng dẫn giải

Đáp án đúng là: D

$\sqrt[3]{16\text{x}-5}$ xác định với mọi số thực x vì 16x – 5 xác định với mọi số thực x.

Bài 5.Biểu thức $\sqrt{\frac{{\left(-5\right)}^2}{6-3\text{x}}}$ có nghĩa khi:

A. x < 2;

B. x > 2;

C. x ≤ 2;

D. x ≥ 2.

Hướng dẫn giải

Đáp án đúng là: A

Biểu thức $\sqrt{\frac{{\left(-5\right)}^2}{6-3\text{x}}}$ có nghĩa khi 6 – 3x ≠ 0 và $\frac{{\left(-5\right)}^2}{6-3\text{x}}\ge 0.$

⦁6 – 3x ≠ 0, hay 3x ≠ 6 nên x ≠ 2;

⦁ $\frac{{\left(-5\right)}^2}{6-3\text{x}}\ge 0$ khi 6 – 3x > 0 (vì (–5)² > 0), hay 3x < 6 nên x < 2.

Kết hợp hai điều kiện trên ta được x < 2.

Vậy biểu thức $\sqrt{\frac{{\left(-5\right)}^2}{6-3\text{x}}}$ có nghĩa khi x < 2.

Bài 6. Có bao nhiêu số tự nhiên x để $\sqrt{16-x}$ là số nguyên?

A. 2;

B. 3;

C. 4;

D. 5.

Hướng dẫn giải

Đáp án đúng là: D

Biểu thức $\sqrt{16-x}$ có nghĩa thì 16 – x ≥ 0.

Mà x là số tự nhiên nên x ≥ 0, suy ra 16 – x ≤ 16.

Do đó 0 ≤ 16 – x ≤ 16. (1)

Để $\sqrt{16-x}$ là số nguyên thì 16 – x phải là số chính phương.

Từ (1) và (2) suy ra 16 – x ∈ {0; 1; 4; 9; 16}.

Do đó x – 16 ∈ {0; –1; –4; –9; –16}

Nên x ∈ {16; 15; 12; 7; 0}.

Vậy có 5 giá trị của x thỏa mãn yêu cầu đề bài.

Bài 7.Cho hai biểu thức A và B. Khẳng định nào sau đây là đúng?

A. $A\sqrt{B}=\sqrt{A^{2}B}$ với mọi A, B;

B. $\sqrt{A^2}=-A$ khi A < 0;

C. $\sqrt{A{B}^2}=-B\sqrt{A}$ khi A ≥ 0 và B ≥ 0;

D. $\sqrt{-AB}=-\sqrt{A}\cdot \sqrt{B}$ khi A ≥ 0 và B ≥ 0.

Hướng dẫn giải

Đáp án đúng là: B

Ta có:

⦁ $\sqrt{A^2}=\left|A\right|=-A$ khi A < 0;

⦁ $A\sqrt{B}=\sqrt{A^{2}B}$ khi A ≥ 0 và B ≥ 0;

⦁ $\sqrt{A{B}^2}=-B\sqrt{A}$ khi A ≥ 0 và B < 0;

⦁ $\sqrt{-AB}=\sqrt{-A}\cdot \sqrt{B}$ khi A < 0 và B ≥ 0 hoặc $\sqrt{-AB}=\sqrt{A}\cdot \sqrt{-B}$ khi A ≥ 0 và B < 0.

Vậy ta chọn phương án B.

Bài 8. Cho các biểu thức A, B, C có giá trị dương. Khẳng định nào sau đây là đúng?

A. $\sqrt{\frac{A}{BC}}=\frac{\sqrt{ABC}}{B};$

B. $\sqrt{\frac{A}{BC}}=-\frac{\sqrt{ABC}}{BC};$

C. $\sqrt{\frac{A}{BC}}=\frac{\sqrt{ABC}}{BC};$

D. $\sqrt{\frac{A}{BC}}=\frac{ABC}{\sqrt{BC}}.$

Hướng dẫn giải

Đáp án đúng là: C

Với A > 0, B > 0, C > 0, ta có:

$\sqrt{\frac{A}{BC}}=\frac{\sqrt{A}}{\sqrt{BC}}=\frac{\sqrt{A}\cdot \sqrt{BC}}{{\left(\sqrt{BC}\right)}^2}=\frac{\sqrt{ABC}}{BC}.$

Vậy ta chọn phương án C.

II. Bài tập tự luận

Bài 1. Tính giá trị của các biểu thức sau:

a) ${\left(\sqrt{58}\right)}^2-\sqrt{{45}^2};$

b) $\frac{2}{7}\sqrt{49}+\frac{26}{3}\sqrt{\frac{81}{169}}-\sqrt{625};$

c) $\sqrt[3]{{\left(-15\right)}^3}+{\left(\sqrt[3]{21}\right)}^3-\sqrt[3]{-27};$

d) $\left(\sqrt{2030}-\sqrt{2029}\right)\left(\sqrt{2030}+\sqrt{2029}\right);$

e) $\left(\sqrt[3]{3}-1\right)\left[{\left(\sqrt[3]{3}\right)}^2+\sqrt[3]{3}+1\right];$

f) $\sqrt{7-4\sqrt{3}};$

g) $\sqrt{\sqrt{5}+3}\cdot \sqrt{3-\sqrt{5}};$

h) $\frac{\sqrt{{\left(6,2\right)}^2-{\left(5,9\right)}^2}}{\sqrt{2,43}};$

i) ${\left(\sqrt{6}-\sqrt{5}\right)}^2+\sqrt{120}.$

Hướng dẫn giải

a) ${\left(\sqrt{58}\right)}^2-\sqrt{{45}^2}=58-45=13.$

b) $\frac{2}{7}\sqrt{49}+\frac{26}{3}\sqrt{\frac{81}{169}}-\sqrt{625}$

$=\frac{2}{7}\cdot 7+\frac{26}{3}\cdot \frac{9}{13}-25$

= 2 + 6 – 25

= –17.

c) $\sqrt[3]{{\left(-15\right)}^3}+{\left(\sqrt[3]{21}\right)}^3-\sqrt[3]{-27}$

= –15 + 21 – 3

= 3.

d)$\left(\sqrt{2030}-\sqrt{2029}\right)\left(\sqrt{2030}+\sqrt{2029}\right)$

$={\left(\sqrt{2030}\right)}^2-{\left(\sqrt{2029}\right)}^2$

= 2 030 – 2 029 = 1.

e) $\left(\sqrt[3]{3}-1\right)\left[{\left(\sqrt[3]{3}\right)}^2+\sqrt[3]{3}+1\right]={\left(\sqrt[3]{3}\right)}^3-1^3=3-1=2.$

f) $\sqrt{7-4\sqrt{3}}=\sqrt{4-2\cdot 2\cdot \sqrt{3}+3}=\sqrt{2^2-2\cdot 2\cdot \sqrt{3}+{\left(\sqrt{3}\right)}^2}$

$=\sqrt{{\left(2-\sqrt{3}\right)}^2}=\left|2-\sqrt{3}\right|=2-\sqrt{3}$ (vì $2-\sqrt{3}>0$ do $2>\sqrt{3}$)

g) $\sqrt{\sqrt{5}+3}\cdot \sqrt{3-\sqrt{5}}=\sqrt{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}$

$=\sqrt{3^2-{\left(\sqrt{5}\right)}^2}=\sqrt{9-5}=\sqrt{4}=2.$

h) $\frac{\sqrt{{\left(6,2\right)}^2-{\left(5,9\right)}^2}}{\sqrt{2,43}}=\frac{\sqrt{\left(6,2-5,9\right)\cdot \left(6,2+5,9\right)}}{\sqrt{2,43}}$

$=\frac{\sqrt{0,3\cdot 12,1}}{\sqrt{2,43}}=\frac{\sqrt{3,63}}{\sqrt{2,43}}=\sqrt{\frac{3,63}{2,43}}=\sqrt{\frac{363}{243}}=\sqrt{\frac{121}{81}}=\frac{11}{9}.$

i) ${\left(\sqrt{6}-\sqrt{5}\right)}^2+\sqrt{120}=6-2\sqrt{6}\cdot \sqrt{5}+5+\sqrt{4\cdot 30}$

$=11-2\sqrt{6\cdot 5}+\sqrt{2^2\cdot 30}=11-2\sqrt{30}+2\sqrt{30}=11.$

Bài 2.Rút gọn biểu thức $P=\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}.$

Hướng dẫn giải

$P=\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}$

$=\left[\frac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\frac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right]:\frac{1}{\sqrt{7}-\sqrt{5}}$

$=\left(-\sqrt{7}-\sqrt{5}\right)\cdot \left(\sqrt{7}-\sqrt{5}\right)$

$=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)$

= –(7 – 5) = –2.

Bài 3. Tìm điều kiện xác định của các biểu thức sau:

a) $\sqrt{3x-36};$

b) $\sqrt{24-3x};$

c) $\sqrt{\frac{2}{x^2}};$

d) $\sqrt{\frac{3}{1-2x}};$

e) $\sqrt{\frac{-10}{2x+4}};$

f) $\sqrt[3]{5-x};$

g) $\sqrt[3]{\frac{1}{x-1}};$

h) $\sqrt[3]{\frac{x-2}{-x^2+x-1}}.$

Hướng dẫn giải

a) Biểu thức $\sqrt{3x-36}$ xác định khi 3x – 36 ≥ 0 hay 3x ≥ 36, tức là x ≥ 12.

b) Biểu thức $\sqrt{24-3x}$xác định khi 24 – 3x ≥ 0 hay 3x ≤ 24, tức là x ≤ 8.

c) Biểu thức $\sqrt{\frac{2}{x^2}}$xác định khi $\frac{2}{x^2}\ge 0,$ hay x² > 0, tức là x ≠ 0.

d) Biểu thức $\sqrt{\frac{3}{1-2x}}$xác định khi $\frac{3}{1-2x}\ge 0,$ hay 1 – 2x > 0, tức là

e) Biểu thức $\sqrt{\frac{-10}{2x+4}}$xác định khi $\frac{-10}{2x+4}\ge 0,$ hay 2x + 4 < 0, tức là x < –2.

f) Biểu thức $\sqrt[3]{5-x}$xác định với mọi số thực x vì 5 – x xác định với mọi số thực x.

g) Biểu thức $\sqrt[3]{\frac{1}{x-1}}$xác định khi $\frac{1}{x-1}$ xác định, có nghĩa là x – 1 ≠ 0, hay x ≠ 1.

h) Biểu thức $\sqrt[3]{\frac{x-2}{-x^2+x-1}}$xác định khi $\frac{x-2}{-x^2+x-1}$ xác định, có nghĩa là –x² + x – 1 ≠ 0.

Ta có: $-x^2+x-1=-\left(x^2-2\cdot x\cdot \frac{1}{2}+\frac{1}{4}\right)-\frac{3}{4}=-{\left(x-\frac{1}{2}\right)}^2-\frac{3}{4}.$

Với mọi số thực x, ta có ${\left(x-\frac{1}{2}\right)}^2\ge 0,$ nên $-{\left(x-\frac{1}{2}\right)}^2\le 0,$ suy ra $-{\left(x-\frac{1}{2}\right)}^2-\frac{3}{4}\le -\frac{3}{4}$

Do đó $-{\left(x-\frac{1}{2}\right)}^2-\frac{3}{4}\ne 0$ với mọi số thực x hay biểu thức $\sqrt[3]{\frac{x-2}{-x^2+x-1}}$ xác định với mọi số thực x.

Bài 4.Rút gọn các biểu thức sau:

a) $\sqrt{225\left(x^2-4x+4\right)}$ với x ≥ 2;

b) $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}$ với x < y.

Hướng dẫn giải

a) Ta có: $\sqrt{225\left(x^2-4x+4\right)}=\sqrt{{15}^2\cdot {\left(x-2\right)}^2}$

 $=\sqrt{{15}^2}\cdot \sqrt{{\left(x-2\right)}^2}=15\left|x-2\right|.$

Với x ≥ 2 thì x – 2 ≥ 0  nên |x – 2| = x – 2.

Do đó $\sqrt{225\left(x^2-4x+4\right)}=15\left|x-2\right|=15\left(x-2\right)=15x-30$

Vậy  với x ≥ 2.

b) Cách 1:

Ta có:  $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=\frac{3}{x-y}\sqrt{x^4}\cdot \sqrt{{\left(x-y\right)}^2}=\frac{3}{x-y}\cdot x^2\left|x-y\right|$

Với x < y thì x – y < 0 nên |x – y| = – (x – y).

Do đó $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=\frac{3}{x-y}\cdot x^2\left|x-y\right|=\frac{3}{x-y}\cdot x^2\cdot \left[-\left(x-y\right)\right]=-3x^2.$

Vậy $\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=-3x^2$  với x < y.

Cách 2: Với x < y thì x – y < 0 nên ta có:

$\frac{3}{x-y}\sqrt{x^4{\left(x-y\right)}^2}=3\cdot \sqrt{x^4}\cdot \frac{1}{x-y}\cdot \sqrt{{\left(x-y\right)}^2}$

$=-3x^2\sqrt{\frac{1}{{\left(x-y\right)}^2}\cdot {\left(x-y\right)}^2}=-3x^2.$

Bài 5.Tìm x, biết:

a) $\sqrt{x}=\frac{1}{2};$

b) $\sqrt[3]{x-10}=5;$

c) $5\sqrt{8-4\text{x}}-2\sqrt{32-16\text{x}}=10.$

Hướng dẫn giải

a) Điều kiện xác định x ≥ 0.

$\sqrt{x}=\frac{1}{2}$

${\left(\sqrt{x}\right)}^2={\left(\frac{1}{2}\right)}^2$

$x=\frac{1}{4}$ (thỏa mãn điều kiện).

Vậy $x=\frac{1}{4}$

b) $\sqrt[3]{x-10}=5$

${\left(\sqrt[3]{x-10}\right)}^3=5^3$

x – 10 = 125

x = 135

Vậy x = 135.

c) Điều kiện xác định x ≤ 2.

$5\sqrt{8-4\text{x}}-2\sqrt{32-16\text{x}}=10$

$5\sqrt{4\left(2-\text{x}\right)}-2\sqrt{16\left(2-\text{x}\right)}=10$

$10\sqrt{\left(2-\text{x}\right)}-8\sqrt{\left(2-\text{x}\right)}=10$

$2\sqrt{\left(2-\text{x}\right)}=10$

$\sqrt{\left(2-\text{x}\right)}=5$

2 – x = 25

x = –23 (thỏa mãn điều kiện).

Vậy x = –23.

Bài 6.Cho $A=\left(\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{x\sqrt{x}-8}\right):\left(\frac{\sqrt{x}+7}{x+2\sqrt{x}+4}\right)$ với x ≥ 0, x ≠ 4.

a) Rút gọn biểu thức A.

b) Tìm x sao cho A < 2.

Hướng dẫn giải

a)Với x ≥ 0, x ≠ 4, ta có:

$A=\left(\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{x\sqrt{x}-8}\right):\left(\frac{\sqrt{x}+7}{x+2\sqrt{x}+4}\right)$

$=\left[\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{x-3}{x+2\sqrt{x}+4}-\frac{7\sqrt{x}+10}{{\left(\sqrt{x}\right)}^3-2^3}\right]\cdot \frac{x+2\sqrt{x}+4}{\sqrt{x}+7}$

$=\frac{\sqrt{x}\left(x+2\sqrt{x}+4\right)-\left(x-3\right)\left(\sqrt{x}-2\right)-7\sqrt{x}-10}{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+4\right)}\cdot \frac{x+2\sqrt{x}+4}{\sqrt{x}+7}$

$=\frac{x\sqrt{x}+2x+4\sqrt{x}-x\sqrt{x}+2x+3\sqrt{x}-6-7\sqrt{x}-10}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}$

$=\frac{4x-16}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}=\frac{4\left(x-4\right)}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}$

$=\frac{4\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}-2}\cdot \frac{1}{\sqrt{x}+7}$

$=\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}.$

Vậy với x ≥ 0, x ≠ 4 thì $A=\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}.$

b)Với x ≥ 0, x ≠ 4, ta có A < 2 nên $\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}<2.$

Giải bất phương trình:

$\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}<2.$

$\frac{4\left(\sqrt{x}+2\right)}{\sqrt{x}+7}-2<0$

$\frac{4\left(\sqrt{x}+2\right)-2\left(\sqrt{x}+7\right)}{\sqrt{x}+7}<0$

$4\sqrt{x}+8-2\sqrt{x}-14<0$(Do $\sqrt{x+7}>0)$

$2\sqrt{x}<6$

$\sqrt{x}<3$

x < 9.

Kết hợp điều kiện xác định ta được 0 ≤ x < 9 và x ≠ 4.

Bài 7.Người ta cần làm một cái thùng hình lập phương bằng bìa cứng không có nắp trên và có thể tích 32768 m³. Tính diện tích bìa cứng cần dùng để làm thùng đựng đó (coi diện tích các mép nối là không đáng kể).

Hướng dẫn giải

Cạnh cái thùng hình lập phương là: $\sqrt[3]{32768}=32$ (m).

Cái thùng đó có 5 mặt là 5 hình vuông.

Diện tích bìa cứng phải dùng để làm cái thùng là:

32². 5 = 5 120 (m²).

Bài 8.Công thức $h=0,4\sqrt[3]{x}$ biểu diễn mối tương quan giữa cân nặng x (tính bằng kg) và chiều cao h (tính bằng m) của một con hươu cao cổ.

a) Một con hươu cao cổ cân nặng 195 kg thì cao bao nhiêu mét? (làm tròn kết quả đến hàng phần trăm).

b) Một con hươu cao cổ có chiều cao 2,62 m thì cân nặng bao nhiêu kilôgam? (làm tròn kết quả đến hàng đơn vị).

Hướng dẫn giải

a) Con hươu cao cổ nặng 195 kg thì x = 195.

Thay x = 195 vào công thức $h=0,4\sqrt[3]{x}$ ta được chiều cao của con hươu cao cổ là:

$h=0,4\sqrt[3]{x}=0,4\sqrt[3]{195}\approx 2,32$ (m).

b) Con hươu cao cổ cao 2,62 m thì h = 2,62.

Thay h = 2,62vào công thức $h=0,4\sqrt[3]{x}$ ta được phương trình:

$2,62=0,4\sqrt[3]{x}.$

Giải phương trình:

$2,62=0,4\sqrt[3]{x}$

$\sqrt[3]{x}=6,55$

x ≈ 281 (kg).

Vậy con hươu cao cổ có chiều cao 2,62 m thì cân nặng khoảng 281kg.

Học tốt Bài tập cuối chương 3

Các bài học để học tốt Bài tập cuối chương 3 Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài tập cuối chương 3