Giải Toán 9 trang 105 Tập 1 Cánh diều
Với Giải Toán 9 trang 105 Tập 1 trong Bài 2: Vị trí tương đối của đường thẳng và đường tròn Toán lớp 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 105.
Giải Toán 9 trang 105 Tập 1 Cánh diều
Bài 4 trang 105 Toán 9 Tập 1: Cho bốn điểm O, M, N, P cùng nằm trên một đường thẳng sao cho điểm M nằm giữa hai điểm O và N; điểm N nằm giữa hai điểm M và P. Gọi a, b, c lần lượt là các đường thẳng đi qua M, N, P và vuông góc với đường thẳng OP. Xác định vị trí tương đối của mỗi đường thẳng a, b, c và đường tròn (O; ON).
Lời giải:
– Vì điểm M nằm giữa hai điểm O và N nên OM < ON suy ra khoảng cách từ O đến đường thẳng a nhỏ hơn bán kính của đường tròn (O; ON). Vậy đường thẳng a và đường tròn (O; ON) cắt nhau.
– Vì khoảng cách từ O đến đường thẳng b (là ON) bằng bán kính của đường tròn (O; ON). Vậy đường thẳng b và đường tròn (O; ON) tiếp xúc nhau.
– Vì điểm M nằm giữa hai điểm O và N; điểm N nằm giữa hai điểm M và P nên điểm N nằm giữa hai điểm O và P.
Suy ra OP > ON nên khoảng cách từ O đến đường thẳng c lớn hơn bán kính của đường tròn (O; ON). Vậy đường thẳng b và đường tròn (O; ON) không giao nhau.
Bài 5 trang 105 Toán 9 Tập 1: Cho điểm O và đường thẳng a không đi qua O.
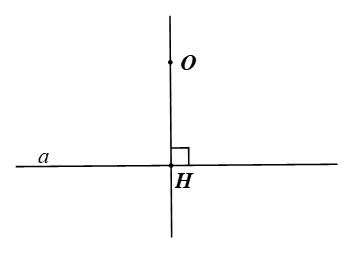
a) Vẽ điểm H là hình chiếu của điểm O trên đường thẳng a.
b) Từ đó, vẽ ba đường tròn tâm O lần lượt: không giao với đường thẳng a; tiếp xúc với đường thẳng a; cắt đường thẳng a tại hai điểm phân biệt.
Lời giải:
a)
b)
Đường tròn (O; OM) không giao với đường thẳng a;
Đường tròn (O: OH) tiếp xúc với đường thẳng a;
Đường tròn (O; OK) cắt đường thẳng a tại hai điểm A và B phân biệt.
Lời giải bài tập Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn hay khác: