Khám phá 3 trang 8 Toán 9 Tập 2 Chân trời sáng tạo

Cho hàm số y = x. Ta lập bảng giá trị sau:

Giải Toán 9 Bài 1: Hàm số và đồ thị của hàm số y = ax^2 (a khác 0) - Chân trời sáng tạo

Khám phá 3 trang 8 Toán 9 Tập 2: Cho hàm số y = x². Ta lập bảng giá trị sau:

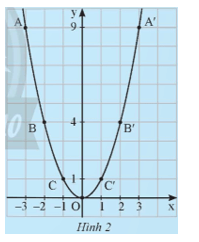
Từ bảng trên, ta lấy các điểm A(−3; 9), B(−2; 4), C(−1; 1), O(0; 0), C'(1; 1), B'(2; 4), A'(3; 9) trên mặt phẳng tọa độ Oxy. Đồ thị hàm số y = x² là một đường cong đi qua các điểm nêu trên và có dạng như Hình 2.

Từ đồ thị ở Hình 2, hãy trả lời các câu hỏi sau:

a) Đồ thị của hàm số có vị trí như thế nào so với trục hoành?

b) Có nhận xét gì về vị trí của các cặp điểm A và A', B và B', C và C' so với trục tung?

c) Điểm nào là điểm thấp nhất của đồ thị?

Lời giải:

a) Từ đồ thị ở Hình 2, ta thấy đồ thị của hàm số có vị trí phía trên so với trục hoành.

b) Xét cặp điểm A(−3; 9) và A'(3; 9), hai điểm này có cùng tung độ và có hoành độ đối nhau nên hai điểm A và A' đối xứng với nhau qua trục tung.

Xét cặp điểm B(−2; 4) và B'(2; 4), hai điểm này có cùng tung độ và có hoành độ đối nhau nên hai điểm B và B' đối xứng với nhau qua trục tung.

Xét cặp điểm C(−1; 1) và C'(1; 1), hai điểm này có cùng tung độ và có hoành độ đối nhau nên hai điểm C và C' đối xứng với nhau qua trục tung.

Vậy các cặp điểm A và A', B và B', C và C' đối xứng với nhau qua trục tung.

c) Từ đồ thị ở Hình 2, ta thấy điểm thấp nhất của đồ thị là điểm O(0; 0).

Lời giải bài tập Toán 9 Bài 1: Hàm số và đồ thị của hàm số y = ax^2 (a khác 0) hay, chi tiết khác:

• Khởi động trang 6 Toán 9 Tập 2: Một vật được thả rơi tự do từ độ cao 45 m. Quãng đường chuyển động s (m) của vật theo thời gian rơi t ...

• Khám phá 1 trang 6 Toán 9 Tập 2: Diện tích S của hình tròn được tính bởi công thức S = πR², trong đó R là bán kính của hình tròn và π ≈ 3,14.....

• Thực hành 1 trang 7 Toán 9 Tập 2: a) Xác định hệ số của x² trong các hàm số sau: $y=0,75x^2;y=-3x^2;y=\frac{1}{4}{x}^2.$....

• Vận dụng 1 trang 7 Toán 9 Tập 2: Gọi x (cm) là chiều dài cạnh của một viên gạch lát nền hình vuông.....

• Khám phá 2 trang 7 Toán 9 Tập 2: Cho hàm số $y=\frac{1}{2}{x}^2.$ Hoàn thành bảng giá trị sau:....

• Thực hành 2 trang 8 Toán 9 Tập 2: Lập bảng giá trị của hai hàm số $y=\frac{1}{4}{x}^2$ và $y=-\frac{1}{4}{x}^2$ với x lần lượt bằng $-4;-2;0;2;4.$....

• Vận dụng 2 trang 8 Toán 9 Tập 2: Một vật rơi tự do từ độ cao 125 m so với mặt đất. Quãng đường chuyển động s (m) của vật phụ thuộc vào thời gian t ....

• Khám phá 4 trang 8 Toán 9 Tập 2: Cho hàm số $y=-\frac{3}{2}{x}^2.$a) Lập bảng giá trị của hàm số khi x lần lượt nhận các giá trị −2; −1; 0; 1; 2.....

• Thực hành 3 trang 9 Toán 9 Tập 2: Vẽ đồ thị của hàm số y = 2x².....

• Vận dụng 3 trang 10 Toán 9 Tập 2: Động năng (tính bằng J) của một quả bưởi nặng 1 kg rơi với vận tốc v (m/s) được tính bằng công thức ....

• Bài 1 trang 10 Toán 9 Tập 2: Cho hàm số y = −x². Lập bảng giá trị của hàm số....

• Bài 2 trang 10 Toán 9 Tập 2: Cho hàm số $y=\frac{1}{2}{x}^2.$ Vẽ đồ thị của hàm số.....

• Bài 3 trang 10 Toán 9 Tập 2: Cho hai hàm số $y=\frac{1}{4}{x}^2$ và $y=-\frac{1}{4}{x}^2.$ Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ Oxy....

• Bài 4 trang 10 Toán 9 Tập 2: Cho hàm số y = ax² (a ≠ 0). Tìm a, biết đồ thị của hàm số đi qua điểm M(2; 6).....

• Bài 5 trang 10 Toán 9 Tập 2: Cho một hình lập phương có độ dài cạnh x (cm).....

• Bài 6 trang 10 Toán 9 Tập 2: Khi gió thổi vuông góc vào cánh buồm của một con thuyền thì lực F (N) của nó tỉ lệ thuận với bình phương tốc độ v ....