Khám phá 3 trang 95 Toán 9 Tập 2 Chân trời sáng tạo
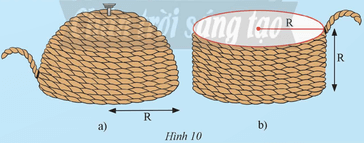
Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R.
Giải Toán 9 Bài 3: Hình cầu - Chân trời sáng tạo
Khám phá 3 trang 95 Toán 9 Tập 2: Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R.
a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b.
b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.
Lời giải:
a) Diện tích xung quanh của phần hình trụ là: S = 2πR . R = 2πR2.
Vậy diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b là 2πR2.
b) Theo đề bài, chiều cao của phần hình trụ được quấn dây bằng bán kính R.
Dự đoán: Diện tích nửa mặt cầu là 2πR2.
Lời giải bài tập Toán 9 Bài 3: Hình cầu hay, chi tiết khác:
Khám phá 1 trang 93 Toán 9 Tập 2: Cho tấm bìa có dạng nửa hình tròn tâm O và đường kính AB ....
Khám phá 2 trang 94 Toán 9 Tập 2: Quan sát Hình 5 và cho biết mặt cắt quả cam có dạng hình gì ....
Khám phá 4 trang 96 Toán 9 Tập 2: Một quả cầu có bán kính R nằm khít trong chiếc bình hình trụ ....
Thực hành 3 trang 96 Toán 9 Tập 2: Một quả bóng rổ (khi bơm căng) có đường kính 24 cm (Hình 14) ....
Bài 1 trang 96 Toán 9 Tập 2: Đồ vật nào sau đây có dạng hình cầu? ....
Bài 4 trang 97 Toán 9 Tập 2: Cắt một hình cầu có bán kính 5 cm bằng một mặt phẳng đi qua tâm ....