Giải Toán 9 trang 99 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 99 Tập 2 trong Bài tập cuối chương 10 Toán 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 99.

Giải Toán 9 trang 99 Tập 2 Chân trời sáng tạo

Bài 11 trang 99 Toán 9 Tập 2: Người ta cần sơn mặt bên trong của một chao đèn có dạng hình nón (không tính đáy) với bán kính đáy là 20 cm, độ dài đường sinh là 30 cm (Hình 1c). Hỏi diện tích cần sơn là bao nhiêu?

Lời giải:

Diện tích cần sơn là:

S_xq = πrl = π . 20 . 30 ≈ 1 885 (cm²).

Vậy diện tích cần sơn khoảng 1 885 cm².

Bài 12 trang 99 Toán 9 Tập 2: Bạn Nam được tặng một quả bóng đá có đường kính 24 cm (Hình 2). Em hãy giúp bạn ấy tính xem cần bao nhiêu diện tích da để làm bóng, giả sử rằng diện tích các mép nối không đáng kể.

Lời giải:

Bán kính của quả bóng là: $R=\frac{24}{2}=12\left(cm\right).$

Diện tích da để làm quả bóng là:

S = 4πR² = 4π . 12² ≈ 1 810 (cm²).

Vậy diện tích da để làm bóng khoảng 1 810 cm².

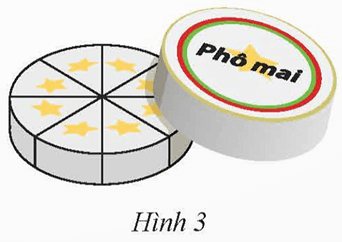
Bài 13 trang 99 Toán 9 Tập 2: Hộp phô mai hình trụ có đường kính đáy 12,2 cm, chiều cao 2,4 cm.

a) Biết rằng 8 miếng phô mai được xếp nằm sát nhau vừa khít trong hộp (Hình 3). Hỏi thể tích một miếng phô mai là bao nhiêu?

b) Người ta gói từng miếng phô mai bằng một loại giấy đặc biệt. Giả sử phần giấy gói vừa khít miếng phô mai. Hãy tính diện tích phần giấy gói mỗi miếng phô mai.

Lời giải:

a) Bán kính đáy hộp phô mai hình trụ là: $R=\frac{d}{2}=\frac{12,2}{2}=6,1\left(cm\right).$

Thể tích hộp phô mai là:

V =πR²h = π . (6,1)². 2,4 ≈ 281 (cm³).

Thể tích một miếng phô mai là:

281 : 8 = 35 (cm³).

Vậy thể tích một miếng phô mai khoảng 35 cm³.

b) Diện tích một mặt đáy của miếng phô mai là:

$S_{đáy}=\frac{\pi \cdot {\left(6,1\right)}^2}{8}=\frac{3721}{800}\pi \left(c{m}^2\right).$

Diện tích một mặt bên hình chữ nhật của miếng phô mai là:

S_bên = 2,4 . 6,1 = 14,64 (cm²).

Diện tích mặt cong của miếng phô mai là:

$S_{cong}=\frac{2\pi \cdot 6,1\cdot 2,4}{8}=3,66\pi \left(c{m}^2\right).$

Diện tích phần giấy gói mỗi miếng phô mai là:

$S=2S_{đáy}+2S_{bên}+S_{cong}=2\cdot \frac{3721}{800}\pi +2\cdot 14,64+3,66\pi \approx 70\left(c{m}^2\right).$

Vậy diện tích phần giấy gói mỗi miếng phô mai khoảng 70 cm².

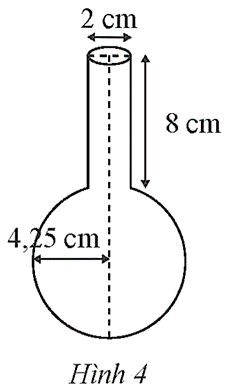
Bài 14 trang 99 Toán 9 Tập 2: Ta coi một ống nghiệm có phần trên là hình trụ và phần dưới là hình cầu (Hình 4). Hãy tính thể tích nước cần để đổ đầy vào ống nghiệm, coi bề dày của ống nghiệm không đáng kể.

Lời giải:

Bán kính phần hình trụ là: r = $\frac{2}{2}$ = 1 (cm).

Thể tích phần hình trụ là: 

V₁ = π . 1² . 8 = 8π (cm³).

Thể tích hình cầu là:

$V_2=\frac{4}{3}\cdot \pi \cdot {\left(4,25\right)}^3=\frac{4913}{48}\pi \left(c{m}^3\right).$

Thể tích nước cần để đổ đầy bình là:

$V=V_1+V_2=8\pi +\frac{4913}{48}\pi \approx 347\left(c{m}^3\right).$

Vậy thể tích nước cần để đổ đầy vào ống nghiệm khoảng 347 cm³.

Bài 15 trang 99 Toán 9 Tập 2: Một hộp bóng hình trụ chứa vừa khít 3 quả bóng tennis có đường kính 6,5 cm (Hình 5).

a) Tính diện tích bề mặt và thể tích của mỗi quả bóng.

b) Tính diện tích xung quanh và thể tích hộp bóng. 

Lời giải:

a) Bán kính quả bóng là: R = $\frac{6,5}{2}$ = 3,25 (cm).

Diện tích bề mặt mỗi quả bóng là: 

S = 4πR² = 4π . 3,25² ≈ 133 (cm²).

Thể tích mỗi quả bóng là:

$V=\frac{4}{3}\cdot \pi \cdot R^3=\frac{4}{3}\cdot \pi \cdot {\left(3,25\right)}^3\approx 144\left(c{m}^3\right).$

Vậy mỗi quả bóng có diện tích bề mặt khoảng 133 cm² và thể tích là 144 cm³.

b) Chiều cao hộp bóng là:

h = 3d = 3. 6,5 = 19,5 (cm).

Diện tích xung quanh hộp là: 

S_xq = 2πrh = 2π . 3,25 . 19,5 ≈ 398 (cm²).

Thể tích hộp bóng là: 

V = πr²h = π . (3,25)² . 19,5 ≈ 647 (cm³).

Vậy hộp bóng có diện tích xung quanh khoảng 398 cm² và thể tích khoảng 647 cm³.

Lời giải bài tập Toán 9 Bài tập cuối chương 10 hay khác:

• Giải Toán 9 trang 98