Giải Toán 9 trang 108 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 108 Tập 2 trong Bài tập cuối chương 10 Toán 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 108.

Giải Toán 9 trang 108 Tập 2 Kết nối tri thức

Bài 10.17 trang 108 Toán 9 Tập 2: Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB ta được một hình trụ có bán kính bằng độ dài đoạn thẳng

A. AB.

B. CD.

C. AD.

D. AC.

Lời giải:

Đáp án đúng là: C

Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB ta được một hình trụ có bán kính đáy bằng độ dài đoạn thẳng AD.

Bài 10.18 trang 108 Toán 9 Tập 2: Cho tam giác ABC vuông tại A có AB = 4 cm, BC = 5 cm. Khi quay tam giác ABC một vòng quanh AC ta được một hình nón có chiều cao bằng

A. 4 cm.

B. 3 cm.

C. 5 cm.

D. 9 cm.

Lời giải:

Đáp án đúng là: A

Khi quay tam giác ABC một vòng quanh cạnh AC, ta được một hình nón có chiều cao là AC.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có: AB² + AC² = BC².

Suy ra AC² = BC² – AB² = 5² – 4² = 9, do đó AC = 3 cm.

Bài 10.19 trang 108 Toán 9 Tập 2: Diện tích mặt cầu có đường kính 10 cm là

A. 10π cm².

B. 400π cm².

C. 50π cm².

D. 100π cm².

Lời giải:

Đáp án đúng là: D

Bán kính của mặt cầu là: $R=\frac{10}{2}=5\left(cm\right)$.

Diện tích mặt cầu là: S = 4π . 5² = 100π (cm²).

Vậy diện tích mặt cầu có đường kính 10 cm là 100π cm².

Bài 10.20 trang 108 Toán 9 Tập 2: Cho hình nón có bán kính đáy R = 2 cm, độ dài đường sinh ℓ = 5 cm. Diện tích xung quanh của hình nón đã cho bằng

A. $\frac{10\pi }{3}c{m}^2.$

B. $\frac{50\pi }{3}c{m}^2.$

C. 20π cm².

D. 10π cm².

Lời giải:

Đáp án đúng là: D

Diện tích xung quanh hình nón là:

S = π . 2 . 5 = 10π (cm²).

Vậy diện tích xung quanh của hình nón đã cho bằng 10π cm².

Bài 10.21 trang 108 Toán 9 Tập 2: Một mặt phẳng đi qua tâm hình cầu, cắt hình cầu theo một hình tròn có diện tích 9π cm². Thể tích của hình cầu bằng

A. 972π cm³.

B. 36π cm³.

C. 6π cm³.

D. 81π cm³.

Lời giải:

Đáp án đúng là: B

Vì hình tròn đi qua tâm hình cầu có diện tích 9π cm² nên πR² = 9π.

Khi đó, bán kính hình tròn đi qua tâm là R = 3.

Thể tích hình cầu là: $V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi \cdot 3^3=36\pi \left(c{m}^3\right)$.

Vậy thể tích của hình cầu bằng 36π cm³.

Bài 10.22 trang 108 Toán 9 Tập 2: Cho hình trụ có bán kính đáy bằng 20 cm, chiều cao bằng 30 cm.

a) Tính diện tích xung quanh của hình trụ.

b) Tính thể tích của hình trụ.

Lời giải:

a) Diện tích xung quanh hình trụ là:

S_xq = 2π . 20 . 30 = 1 200π (cm²).

Vậy diện tích xung quanh của hình trụ là 1 200π cm².

b) Thể tích hình trụ là:

V = π . 20². 30 = 12 000π (cm³).

Vậy thể tích của hình trụ là 12 000π cm³.

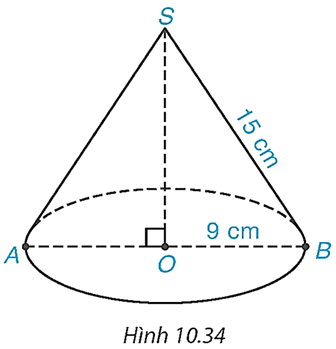
Bài 10.23 trang 108 Toán 9 Tập 2: Cho hình nón có bán kính đáy bằng 9 cm, độ dài đường sinh bằng 15 cm (H.10.34).

a) Tính diện tích xung quanh của hình nón.

b) Tính thể tích của hình nón.

c) Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy. Tính diện tích toàn phần của hình nón đã cho.

Lời giải:

Xét hình nón có đường sinh SB = 15 cm và bán kính đáy OB = 9 cm.

Tam giác SOB vuông tại O nên SO² + OB² = SB² (theo định lí Pythagore)

Suy ra SO² = SB² − OB² = 15² − 9² = 144 nên SO = 12 cm.

a) Diện tích xung quanh của hình nón là:

S_xq = π . OB . SB = 9 . 15 . π = 135π (cm²).

Vậy diện tích xung quanh của hình nón là 135π cm².

b) Thể tích của hình nón là:

$V=\frac{1}{3}\pi \cdot O{B}^2\cdot SO=\frac{1}{3}\pi \cdot 9^2\cdot 12=324\pi \left(c{m}^3\right)$.

c) Diện tích đáy hình nón là:

S_đáy = π . OB² = π . 9² = 81π (cm²).

Diện tích toàn phần của hình nón là:

S = S_xq + S_đáy = 135π + 81π = 216π (cm²).

Vậy diện tích toàn phần của hình nón đã cho là 216π cm².

Lời giải bài tập Toán 9 Bài tập cuối chương 10 hay khác:

• Giải Toán 9 trang 109

• Giải Toán 9 trang 110