Giải Toán 9 trang 109 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 109 Tập 2 trong Bài tập cuối chương 10 Toán 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 109.

Giải Toán 9 trang 109 Tập 2 Kết nối tri thức

Bài 10.24 trang 109 Toán 9 Tập 2: Quả bóng rổ sử dụng trong thi đấu có dạng hình cầu với đường kính bằng 24 cm (H.10.35). Hãy tính:

a) Diện tích bề mặt quả bóng.

b) Thể tích của quả bóng.

Lời giải:

Bán kính quả bóng là: $R=\frac{24}{2}=12\left(cm\right).$

a) Diện tích bề mặt quả bóng là:

V = 4π . R² = 4π . 12² = 576π (cm²).

Vậy diện tích bề mặt quả bóng là 576π cm².

b) Thể tích của quả bóng là:

$V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi \cdot {12}^3=2304\pi \left(c{m}^3\right)$

Vậy thể tích của quả bóng là 2 304π cm³.

Bài 10.25 trang 109 Toán 9 Tập 2: Đèn trời có dạng hình trụ không có một đáy với đường kính đáy bằng 0,8 m và thân đèn cao 1 m (H.10.36). Tính diện tích giấy đèn bên ngoài đèn trời (coi các mép dán không đáng kể).

Lời giải:

Bán kính đáy đèn trời là: $R=\frac{0,8}{2}=0,4\left(cm\right).$

Diện tích xung quanh của đèn trời là:

S_xq = 2πRh = 2π . 0,4 . 1 = 0,8π (m²).

Diện tích đáy hình trụ là:

S_đáy = πR² = π . 0,42 = 0,16π (m²).

Diện tích giấy dán bên ngoài đèn trời:

S = S_đáy + S_xq = 0,16π + 0,8π = 0,96π (m²).

Vậy diện tích giấy đèn bên ngoài đèn trời là 0,96π cm².

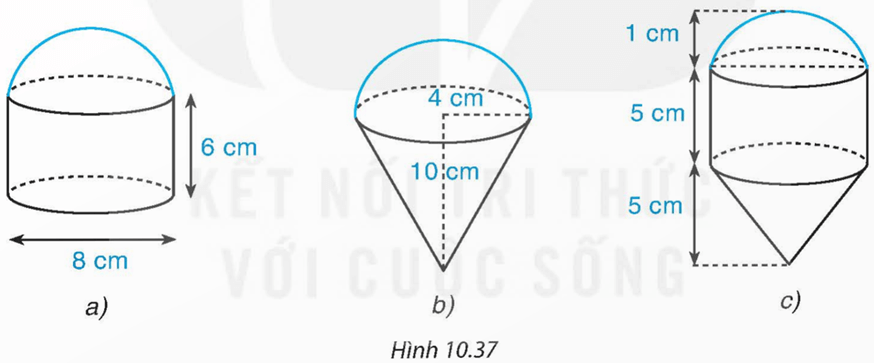
Bài 10.26 trang 109 Toán 9 Tập 2: Các hình dưới đây (H.10.37) được tạo thành từ các nửa hình cầu, hình trụ và hình nón (có cùng bán kính đáy). Tính thể tích của các hình đó theo kích thước đã cho.

Lời giải:

• Xét Hình 10.37 a):

Bán kính đường tròn đáy là: $R=\frac{8}{2}=4\left(cm\right).$

Thể tích của hình trụ có bán kính 4 cm, chiều cao 6 cm là:

V₁ = π . 4² . 6 = 96π (cm³).

Thể nửa hình cầu có bán kính 4 cm là:

$V_2=\frac{1}{2}\cdot \frac{4}{3}\pi \cdot 4^3=\frac{128}{3}\pi \left(c{m}^3\right)$.

Thể tích Hình 10.37 a) là:

$V=V_1+V_2=96\pi +\frac{128}{3}\pi =\frac{416\pi }{3}\left(c{m}^3\right)$.

• Xét Hình 10.37 b):

Thể tích của hình trụ có bán kính 4 cm, chiều cao 10 cm là:

$V_1=\frac{1}{3}\pi \cdot 4^2\cdot 10=\frac{160\pi }{3}\left(c{m}^3\right)$

Thể nửa hình cầu có bán kính 4 cm là:

$V_2=\frac{1}{2}\cdot \frac{4}{3}\pi \cdot 4^3=\frac{128}{3}\pi \left(c{m}^3\right)$.

Thể tích Hình 10.37 b) là:

$V=V_1+V_2=\frac{160\pi }{3}+\frac{128}{3}\pi =96\pi \left(c{m}^3\right)$.

• Xét Hình 10.37 c):

Thể tích của hình trụ có bán kính đáy 1 cm, chiều cao 5 cm là:

V₁ = π . 1² . 5 = 5π (cm³).

Thể tích của hình nón có bán kính đáy 1 cm, chiều cao 5 cm là:

$V_2=\frac{1}{3}\pi \cdot 1^2\cdot 5=\frac{5\pi }{3}\left(c{m}^3\right)$.

Thể tích nửa hình cầu có bán kính 1 cm là:

$V_3=\frac{1}{2}\cdot \frac{4}{3}\pi \cdot 1^3=\frac{2\pi }{3}\left(c{m}^3\right)$

Thể tích Hình 10.37 c) là:

$V=V_1+V_2+V_3=5\pi +\frac{5\pi }{3}+\frac{2\pi }{3}=\frac{22\pi }{3}\left(c{m}^3\right)$.

Vậy trong Hình 10.37: thể tích hình a là $\frac{416\pi }{3}c{m}^3$; thể tích hình b là 96π cm³; thể tích hình c là $\frac{22\pi }{3}c{m}^3.$

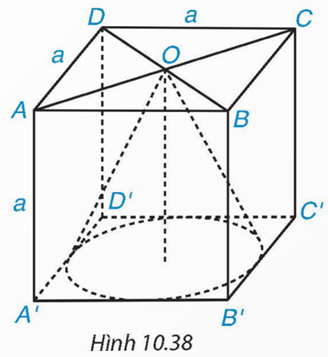
Bài 10.27 trang 109 Toán 9 Tập 2: Cho hình lập phương ABCD.A'B'C'D' cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn tiếp xúc với các cạnh của hình vuông A'B'C'D'. (H.10.38).

Lời giải:

Hình nón đã cho có chiều cao h = a (đvđd).

Vì đáy hình nón là đường tròn nội tiếp hình vuông A'B'C'D' nên bán kính đáy là:

$R=\frac{A^{\text{'}}{B}^{\text{'}}}{2}=\frac{a}{2}$ (đvđd).

Thể tích của hình nón là: $V=\frac{1}{3}\pi R^{2}h=\frac{1}{3}\pi \cdot {\left(\frac{a}{2}\right)}^2\cdot h=\frac{a^3\pi }{12}$ (đvtt).

Vậy thể tích của hình nón đã cho là $\frac{a^3\pi }{12}$ (đvtt).

Lời giải bài tập Toán 9 Bài tập cuối chương 10 hay khác:

• Giải Toán 9 trang 108

• Giải Toán 9 trang 110