Giải Toán 9 trang 127 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 127 Tập 2 trong Bài tập ôn tập cuối năm Toán 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 127.

Giải Toán 9 trang 127 Tập 2 Kết nối tri thức

Bài 1 trang 127 Toán 9 Tập 2: Xét biểu thức $P=\frac{x\sqrt{x}-x+2\sqrt{x}+4}{x\sqrt{x}+8}$ với x ≥ 0.

a) Chứng minh rằng $P=1-\frac{1}{\sqrt{x}+2}.$

b) Tính giá trị biểu thức đã cho tại x = 64.

Lời giải:

a) Với x ≥ 0, ta có:

$P=\frac{x\sqrt{x}-x+2\sqrt{x}+4}{x\sqrt{x}+8}$

$=\frac{x\sqrt{x}+8-\left(x-2\sqrt{x}+4\right)}{\sqrt{x}+8}$

$=1-\frac{x-2\sqrt{x}+4}{\sqrt{x}+8}$

$=1-\frac{x-2\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(x-2\sqrt{x}+4\right)}$

$=1-\frac{1}{\sqrt{x}+2}.$

Vậy với x ≥ 0 thì $P=1-\frac{1}{\sqrt{x}+2}.$

b) Thay x = 64 (thỏa mãn x ≥ 0) vào biểu thức $P=1-\frac{1}{\sqrt{x}+2},$ ta được:

$P=1-\frac{1}{\sqrt{64}+2}=1-\frac{1}{8+2}=1-\frac{1}{10}=\frac{9}{10}.$

Vậy giá trị của biểu thức P bằng $\frac{9}{10}$ khi x = 64.

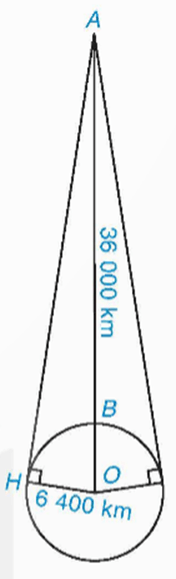
Bài 2 trang 127 Toán 9 Tập 2: Một vệ tinh địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất khoảng AB = 36 000 km, tâm quỹ đạo trùng với tâm O của Trái Đất như hình bên. Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một số vị trí trên bề mặt Trái Đất. Cho biết bán kính Trái Đất khoảng 6 400 km, vị trí xa nhất trên bề mặt Trái Đất có thể nhận được tín hiệu từ vệ tinh cách vệ tinh bao nhiêu kilômét? (Làm tròn kết quả đến hàng đơn vị của km).

Lời giải:

Áp dụng định lí Pythagore cho tam giác AHO vuông tại H, ta có:

AO² = AH² + HO²

Suy ra AH² = AO² – HO² = (AB + BO)² – HO²

                   = (36 000 + 6 400)² – 6 400²

                   = 42 400² – 6 400² = 1 756 800 000.

Do đó AH ≈ 41 914 (km).

Vậy vị trí xa nhất trên bề mặt Trái Đất có thể nhận được tín hiệu từ vệ tinh cách vệ tinh khoảng 41 914 kilômét.

Bài 3 trang 127 Toán 9 Tập 2: Giải các bất phương trình sau:

a) –6x + 3(x + 1) > 4x – (x – 4);

b) (2x + 1)(2x – 1) < 4x² – 4x + 1.

Lời giải:

a) –6x + 3(x + 1) > 4x – (x – 4)

–6x + 3x + 3 > 4x – x + 4

–3x + 3 > 3x + 4

–3x – 3x > 4 – 3

–6x > 1

    $x<-\frac{1}{6}.$

Vậy bất phương trình có nghiệm là $x<-\frac{1}{6}.$

b) (2x + 1)(2x – 1) < 4x² – 4x + 1

4x² – 1 < 4x² – 4x + 1

4x² – 4x² + 4x  < 1 + 1

4x < 2

$x<\frac{1}{2}.$

Vậy bất phương trình có nghiệm là $x<\frac{1}{2}.$

Bài 4 trang 127 Toán 9 Tập 2: Giải các phương trình sau:

a) $\frac{2}{x+1}-\frac{2x}{x^2-x+1}=\frac{3}{x^3+1};$

b) $\frac{x+1}{2x-1}-\frac{2}{2x+1}=\frac{2x^2}{4x^2-1}.$

Lời giải:

a) Điều kiện xác định: x ≠ –1.

$\frac{2}{x+1}-\frac{2x}{x^2-x+1}=\frac{3}{x^3+1}$

$\frac{2\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}-\frac{2x\cdot \left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\frac{3}{\left(x+1\right)\left(x^2-x+1\right)}$

2(x² – x + 1) – 2x(x + 1) = 3

2x² – 2x + 2 – 2x² – 2x = 3

–4x + 2 = 3

–4x = 1

$x=-\frac{1}{4}$ (thỏa mãn điều kiện).

Vậy phương trình đã cho có nghiệm là $x=-\frac{1}{4}$.

b) Điều kiện xác định: $x\ne \frac{1}{2}$ và $x\ne -\frac{1}{2}$

$\frac{x+1}{2x-1}-\frac{2}{2x+1}=\frac{2x^2}{4x^2-1}$

$\frac{\left(x+1\right)\left(2x+1\right)}{\left(2x-1\right)\left(2x+1\right)}-\frac{2\left(2x-1\right)}{\left(2x-1\right)\left(2x+1\right)}=\frac{2x^2}{\left(2x-1\right)\left(2x+1\right)}$

(x + 1)(2x + 1) – 2(2x – 1) = 2x²

2x² + x + 2x + 1 – 4x + 2 = 2x²

2x² – 2x² + x + 2x – 4x = –1 – 2

–x = –3

x = 3 (thỏa mãn điều kiện).

Vậy phương trình đã cho có nghiệm là x = 3.

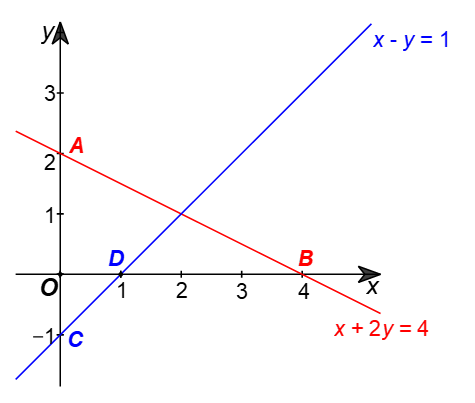
Bài 5 trang 127 Toán 9 Tập 2: Kí hiệu (d₁) là đường thẳng x + 2y = 4, (d₂) là đường thẳng x – y = 1.

a) Vẽ (d₁) và (d₂) trên cùng một mặt phẳng toạ độ.

b) Giải hệ phương trình $\left\{\begin{array}{l}x+2y=4\\ x-y=1\end{array}\right.$ để tìm toạ độ giao điểm của hai đường thẳng (d₁) và (d₂).

Lời giải:

a) ⦁ Vẽ đường thẳng (d₁): x + 2y = 4.

Cho x = 0 thì y = 2, ta được giao điểm của đường thẳng (d₁) với trục tung là A(0; 2).

Cho y = 0 thì x = 4, ta được giao điểm của đường thẳng (d₁) với trục hoành là B(4; 0).

Đường thẳng (d₁) là đường thẳng AB (hình vẽ).

⦁ Vẽ đường thẳng (d₂): x – y = 1.

Cho x = 0 thì y = –1, ta được giao điểm của đường thẳng (d₂) với trục tung là C(0; –1).

Cho y = 0 thì x = 1, ta được giao điểm của đường thẳng (d₂) với trục hoành là D(1; 0).

Đường thẳng (d₂) là đường thẳng CD (hình vẽ).

b) Giải hệ phương trình $\left\{\begin{array}{l}x+2y=4\left(1\right)\\ x-y=1\left(2\right)\end{array}\right.$

Trừ từng vế của hai phương trình (1) và (2), ta được:

(x + 2y) – (x – y) = 4 – 1 hay 3y = 3, suy ra y = 1.

Thế y = 1 vào phương trình (2), ta được:

x – 1 = 1 hay x = 2.

Do đó hệ phương trình trên có nghiệm là (2; 1).

Vậy toạ độ giao điểm của hai đường thẳng (d₁) và (d₂) là điểm (2; 1).

Bài 6 trang 127 Toán 9 Tập 2: Với mỗi giá trị đã cho của m, hãy giải hệ phương trình sau:

$\left\{\begin{array}{l}x\sqrt{2}-3y=m\\ m^{2}x-3y\sqrt{2}=2.\end{array}\right.$

a) m = $\sqrt{2}$.

b) m = -$\sqrt{2}$.

c) m = 2$\sqrt{2}$.

Lời giải:

a) Với m = $\sqrt{2}$ ta có hệ phương trình: $\left(I\right)\left\{\begin{array}{l}x\sqrt{2}-3y=\sqrt{2}\left(1\right)\\ 2x-3y\sqrt{2}=2\end{array}\right.$

Nhân hai vế của phương trình (1) với $\sqrt{2}$ ta được hệ phương trình sau:

$\left\{\begin{array}{l}2x-3y\sqrt{2}=2\\ 2x-3y\sqrt{2}=2.\end{array}\right.$

Trừ từng vế hai phương trình của hệ mới, ta được:

0x + 0y = 0. Hệ thức này luôn thỏa mãn với các giá trị tùy ý của x và y.

Với giá trị tùy ý của x, giá trị của y được tính nhờ hệ thức x$\sqrt{2}$ - 3y = $\sqrt{2}$, suy ra $y=\frac{\sqrt{2}}{3}x-\frac{\sqrt{2}}{3}.$

Vậy hệ phương trình (I) có nghiệm là $\left(x;\frac{\sqrt{2}}{3}x-\frac{\sqrt{2}}{3}\right)$ với x ∈ ℝ.

b) Với m = -$\sqrt{2}$ ta có hệ phương trình: $\left(II\right)\left\{\begin{array}{l}x\sqrt{2}-3y=-\sqrt{2}\left(2\right)\\ 2x-3y\sqrt{2}=2\end{array}\right.$

Nhân hai vế của phương trình (2) với $\sqrt{2}$ ta được hệ phương trình sau:

$\left\{\begin{array}{l}2x-3y\sqrt{2}=-2\\ 2x-3y\sqrt{2}=2.\end{array}\right.$

Trừ từng vế hai phương trình của hệ mới, ta được:

0x + 0y = –4. Phương trình này vô nghiệm.

Vậy hệ phương trình (II) vô nghiệm.

c) Với m = 2$\sqrt{2}$ ta có hệ phương trình: $\left(III\right)\left\{\begin{array}{l}x\sqrt{2}-3y=2\sqrt{2}\left(3\right)\\ 8x-3y\sqrt{2}=2\end{array}\right.$

Nhân hai vế của phương trình (3) với $\sqrt{2}$ ta được hệ phương trình sau:

$\left\{\begin{array}{l}2x-3y\sqrt{2}=4\\ 8x-3y\sqrt{2}=2\end{array}\right.$

Trừ từng vế hai phương trình của hệ mới, ta được:

–6x = 2, suy ra x = -$\frac{1}{3}$

Thế x = -$\frac{1}{3}$ vào phương trình (3), ta được:

$-\frac{1}{3}\cdot \sqrt{2}-3y=2\sqrt{2},$ suy ra $3y=-\frac{\sqrt{2}}{3}-2\sqrt{2},$ nên

$y=-\frac{\sqrt{2}}{9}-\frac{2\sqrt{2}}{3}=\frac{-\sqrt{2}-2\sqrt{2}\cdot 3}{9}=\frac{-7\sqrt{2}}{9}.$

Vậy hệ phương trình (III) có nghiệm là $\left(-\frac{1}{3};\frac{-7\sqrt{2}}{9}\right).$

Bài 7 trang 127 Toán 9 Tập 2: Để chuẩn bị làm một ngôi nhà, chú Ba tính rằng tổng diện tích xây dựng là khoảng 100 m² và tổng chi phí (tiền vật liệu và tiền công thợ) hết khoảng 600 triệu đồng. Khi thực hiện, diện tích xây dựng tăng thêm 20 m² và cứ mỗi mét vuông xây dựng, chi phí tiền vật liệu tăng thêm 10% và tiền công thợ tăng thêm $\frac{1}{5}$ lần so với dự tính ban đầu. Do đó tổng chi phí thực tế là 804 triệu đồng. Hỏi thực tế chú Ba phải trả bao nhiêu tiền vật liệu và bao nhiêu tiền công thợ cho mỗi mét vuông xây dựng?

Lời giải:

Gọi x, y (triệu đồng) lần lượt là số tiền dự tính phải trả vật liệu và công thợ cho mỗi mét vuông xây dựng (0 < x < 600, 0 < y < 600).

+ Theo dự tính, tổng diện tích xây dựng là khoảng 100 m² nên:

⦁ số tiền dùng để trả vật liệu là: 100x (triệu đồng);

⦁ số tiền dùng để trả công thợ là: 100y (triệu đồng).

Do tổng chi phí (tiền vật liệu và tiền công thợ) chú Ba dự tính hết khoảng 600 triệu đồng nên ta có phương trình:

100x + 100y = 600 hay x + y = 6. (1)

+ Theo thực tế:

⦁ tổng diện tích xây dựng là: 100 + 20 = 120 (m²);

⦁ chi phí tiền vật liệu cho mỗi mét vuông là:

(100% + 10%).x = 1,1x (triệu đồng);

⦁ tiền công thợ cho mỗi mét vuông là:

$\left(1+\frac{1}{5}\right)y=1,2y$ (triệu đồng);

⦁ số tiền dùng để trả vật liệu là: 120.1,1x = 132x (triệu đồng);

⦁ số tiền dùng để trả công thợ là: 120.1,2y = 144y (triệu đồng).

Do tổng chi phí thực tế là 804 triệu đồng nên ta có phương trình:

132x + 144y = 804 hay 11x + 12y = 67. (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{\begin{array}{l}x+y=6\left(1\right)\\ 11x+12y=67\left(2\right)\end{array}\right.$

Nhân hai vế của phương trình (1) với 12, ta được hệ phương trình sau:

$\left\{\begin{array}{l}12x+12y=72\\ 11x+12y=67.\end{array}\right.$

Trừ từng vế của hai phương trình trong hệ mới, ta được: x = 5.

Thế x = 5 vào phương trình (1), ta được: 5 + y = 6, suy ra y = 1.

Các giá trị x, y tìm được ở trên đều thỏa mãn điều kiện.

Vậy thực tế chú Ba phải trả 1,1.5 = 5,5 triệu đồng tiền vật liệu và 1,2.1 = 1,2 triệu đồng tiền công thợ cho mỗi mét vuông xây dựng.

Lời giải bài tập Toán 9 Bài tập ôn tập cuối năm hay khác:

• Giải Toán 9 trang 128

• Giải Toán 9 trang 129