Giải Toán 9 trang 128 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 128 Tập 2 trong Bài tập ôn tập cuối năm Toán 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 128.

Giải Toán 9 trang 128 Tập 2 Kết nối tri thức

Bài 8 trang 128 Toán 9 Tập 2: Hai bến A và B trên một dòng sông cách nhau 36 km. Một ca nô xuôi dòng từ bến A đến bến B, rồi sau đó ngược dòng từ bến B về bến A hết thời gian bằng thời gian nó đi quãng đường 75 km khi nước yên lặng. Tính vận tốc thực của ca nô (tức là vận tốc của ca nô khi nước yên lặng), biết rằng vận tốc dòng nước là 3 km/ h.

Lời giải:

Gọi x (km/h) là vận tốc thực của ca nô khi nước yên lặng (x > 3).

Vận tốc của ca nô khi xuôi dòng là: x + 3 (km/h).

Vận tốc của ca nô khi ngược dòng là: x – 3 (km/h).

Thời gian ca nô đi hết quãng đường 75 km khi nước yên lặng là: $\frac{75}{x}$ (giờ).

Thời gian ca nô xuôi dòng từ bến A đến bến B cách nhau 36 km là: $\frac{36}{x+3}$ (giờ).

Thời gian ca nô đi ngược dòng từ bến B về bến A cách nhau 36 km là: $\frac{36}{x-3}$ (giờ).

Do ca nô xuôi dòng từ bến A đến bến B, rồi sau đó ngược dòng từ bến B về bến A hết thời gian bằng thời gian nó đi quãng đường 75 km khi nước yên lặng nên ta có phương trình:

$\frac{36}{x+3}+\frac{36}{x-3}=\frac{75}{x}.$

Giải phương trình:

$\frac{36}{x+3}+\frac{36}{x-3}=\frac{75}{x}$

$\frac{36x\left(x-3\right)}{x\left(x+3\right)\left(x-3\right)}+\frac{36x\left(x+3\right)}{x\left(x+3\right)\left(x-3\right)}=\frac{75\left(x+3\right)\left(x-3\right)}{x\left(x+3\right)\left(x-3\right)}$

36x(x – 3) + 36x(x + 3) = 75(x + 3)(x – 3)

36x² – 108x + 36x² + 108x = 75(x² – 9)

72x² = 75x² – 675

3x² = 675

x² = 225

x = 15 (do x > 3).

Vậy vận tốc thực của ca nô khi nước yên lặng là 15 km/h.

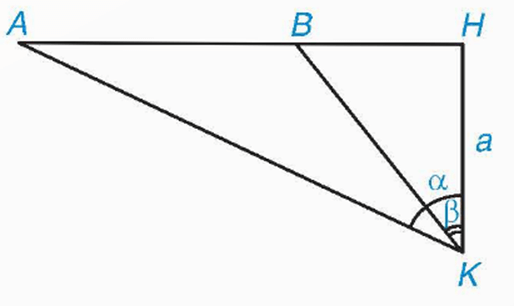
Bài 9 trang 128 Toán 9 Tập 2: Để đo khoảng cách giữa hai điểm A và B không tới được, một người đứng ở điểm H sao cho B ở giữa A và H rồi dịch chuyển đến điểm K sao cho KH vuông góc với AB tại H, HK = a (m), ngắm nhìn A với $\widehat{AKH}=\alpha ,$ ngắm nhìn B với $\widehat{BKH}=\beta \left(\alpha >\beta \right).$

a) Hãy biểu diễn AB theo a, α, β.

b) Khi a = 3 m, α = 60°, β = 30°, hãy tính AB (làm tròn kết quả đến chữ số thập phân thứ ba của mét).

Lời giải:

a) Xét ∆AHK vuông tại H, ta có: AH = HK.tan$\widehat{AKH}$ = a.tan$\alpha$ (m).

Xét BAHK vuông tại H, ta có: BH = HK.tan$\widehat{BKH}=a\cdot tan\beta \left(m\right).$

Do B nằm giữa A và H nên AB + BH = AH.

Suy ra AB = AH – BH = a.tanα – a.tanβ = a(tanα – tanβ) (m).

b) Thay a = 3 m, α = 60°, β = 30° vào biểu thức độ dài AB ở câu a, ta được:

AB = 3.(tan60° – tan30°) $=3\left(\sqrt{3}-\frac{\sqrt{3}}{3}\right)=3\cdot \frac{2\sqrt{3}}{3}=2\sqrt{3}$ ≈ 3,464 (m).

Bài 10 trang 128 Toán 9 Tập 2: Cho tam giác ABC vuông tại B có góc $\widehat{A}=30°$, AB = 6cm. Vẽ tia Bt sao cho $\widehat{tBC}=30°,$ cắt tia AC ở D (C nằm giữa A và D).

a) Chứng minh tam giác ABD cân tại B.

b) Tính khoảng cách từ D đến đường thẳng AB.

Lời giải:

a) Do ∆ABC vuông tại B nên $\widehat{ABC}=90°.$

Ta có: $\widehat{ABD}=\widehat{ABC}+\widehat{tBC}=90°+30°=120°.$

Xét ∆ABD có $\widehat{ABD}+\widehat{BDA}+\widehat{DAB}=180°$ (tổng ba góc của một tam giác).

Suy ra $\widehat{BDA}=180°-\widehat{ABD}-\widehat{DAB}=180°-120°-30°=30°.$

Do đó $\widehat{BAD}=\widehat{BDA}\left(=30°\right)$ nên ∆ABD cân tại B.

b) Vì ∆ABD cân tại B (câu a) nên BD = BA = 6 cm.

Kẻ DH ⊥ AB, H ∈ AB.

Mà BC ⊥ AB nên CB // DH, do đó $\widehat{BDH}=\widehat{tBC}=30°.$

Xét ∆BDH vuông tại H, ta có:

$DH=BD\cdot \cos \widehat{BDH}=6\cdot \cos 30°=6\cdot \frac{\sqrt{3}}{2}=3\sqrt{3}\text{ (cm).}$

Vậy khoảng cách từ D đến đường thẳng AB bằng 3$\sqrt{3}$ cm.

Bài 11 trang 128 Toán 9 Tập 2: Tứ giác ABCD có hai góc đối diện B và D vuông, hai góc kia không vuông.

a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (𝒞).

b) Gọi I và K lần lượt là trung điểm các đường chéo AC và BD của tứ giác. Chứng minh rằng IK ⊥ BD.

c) Kí hiệu các tiếp tuyến của đường tròn (𝒞) tại A, B và C lần lượt là a, b và c. Giả sử b cắt a và c theo thứ tự tại E và F. Chứng minh rằng tứ giác AEFC là một hình thang.

d) Chứng minh rằng EF = AE + CF.

Lời giải:

a) Xét ∆ABC vuông tại B nên đường tròn ngoại tiếp tam giác này có tâm là trung điểm của cạnh huyền AC. Do đó ba điểm A, B, C cùng nằm trên đường tròn đường kính AC.

Xét ∆ADC vuông tại D nên đường tròn ngoại tiếp tam giác này có tâm là trung điểm của cạnh huyền AC. Do đó ba điểm A, D, C cùng nằm trên đường tròn đường kính AC.

Vậy bốn điểm A, B, C và D cùng nằm trên đường tròn đường kính AC.

b) Do đường tròn (𝒞) đi qua bốn điểm A, B, C, D có đường kính là AC mà I là trung điểm của AC nên đường tròn (𝒞) có tâm là I, do đó IB = ID. Suy ra I nằm trên đường trung trực của BD.

Lại có K là trung điểm của BD nên K thuộc đường trung trực của BD.

Vì vậy, IK là đường trung trực của BD nên IK ⊥ BD.

c) Vì đường thẳng a là tiếp tuyến của đường tròn (𝒞) tại A nên IA ⊥ a hay AC ⊥ a.

Vì đường thẳng c là tiếp tuyến của đường tròn (𝒞) tại C nên IC ⊥ c hay AC ⊥ c.

Do đó a // c hay AE // CF nên tứ giác AEFC là hình thang.

d) Xét đường tròn (𝒞) có:

⦁ hai tiếp tuyến tại A và B lần lượt là a, b cắt nhau tại E nên AE = BE.

⦁ hai tiếp tuyến tại C và B lần lượt là c, b cắt nhau tại F nên CF = BF.

Do đó AE + CF = BE + BF = EF.

Vậy EF = AE + CF.

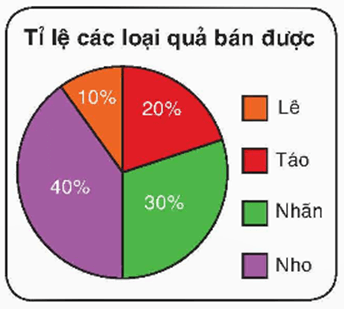
Bài 12 trang 128 Toán 9 Tập 2: Tỉ lệ các loại quả bán được trong một ngày của một cửa hàng được thể hiện trong biểu đồ hình quạt tròn như hình bên. Số phần trăm ghi trong mỗi hình quạt đúng bằng tỉ số giữa số đo của cung tròn tương ứng và số đo của cả đường tròn (360°).

a) Tính số đo của mỗi cung tròn ứng với hình quạt màu tím, màu cam và màu đỏ.

b) Tính số đo của cung còn lại (ứng với hình quạt màu xanh) bằng hai cách.

Lời giải:

a) Số đo của cung tròn ứng với hình quạt màu tím là:

360° . 40% = 144°.

Số đo của cung tròn ứng với hình quạt màu cam là:

360° . 10% = 36°.

Số đo của cung tròn ứng với hình quạt màu đỏ là:

360° . 20% = 72°.

b) Cách 1. Số đo của cung tròn ứng với hình quạt màu xanh là:

360° . 30% = 108°.

Cách 2. Số đo của cung tròn ứng với hình quạt màu xanh là:

360° – 36° – 72° = 108°.

Lời giải bài tập Toán 9 Bài tập ôn tập cuối năm hay khác:

• Giải Toán 9 trang 127

• Giải Toán 9 trang 129