Giải Toán 9 trang 75 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 75 Tập 2 trong Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 75.

Giải Toán 9 trang 75 Tập 2 Kết nối tri thức

Câu hỏi trang 75 Toán 9 Tập 2: Mỗi tam giác có bao nhiêu đường tròn nội tiếp? Có bao nhiêu tam giác cùng ngoại tiếp một đường tròn?

Lời giải:

⦁ Mỗi tam giác chỉ có một đường tròn nội tiếp, vì đối với mỗi góc của tam giác, ta chỉ xác định được duy nhất một đường phân giác, do đó giao điểm của ba đường phân giác này là duy nhất.

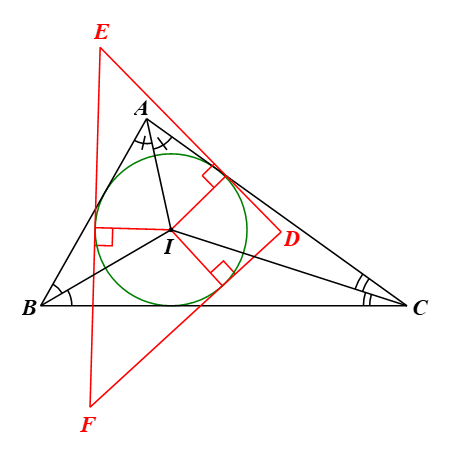
⦁ Có vô số tam giác ngoại tiếp một đường tròn, vì trên đường tròn có vô số điểm, mỗi điểm này đều có thể là một tiếp điểm của đường tròn đó với cạnh của tam giác.

Chẳng hạn như hình vẽ dưới đây:

HĐ6 trang 75 Toán 9 Tập 2: Cho tam giác đều ABC có trọng tâm G.

a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC.

b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa bán kính đường tròn ngoại tiếp tam giác ABC và bằng $\frac{\sqrt{3}}{6}BC.$

Lời giải:

a) Vì ∆ABC là tam giác đều nên ba đường trung tuyến đồng thời là ba đường phân giác, hay trọng tâm G của tam giác cũng là giao điểm của ba đường phân giác của tam giác đó.

Do đó trọng tâm G là tâm đường tròn nội tiếp của tam giác ABC.

b) Vì ∆ABC là tam giác đều nên ba đường trung tuyến đồng thời là ba đường trung trực, hay trọng tâm G của tam giác cũng là giao điểm của ba đường trung trực của tam giác đó.

Do đó trọng tâm G là tâm đường tròn ngoại tiếp của tam giác ABC.

Gọi M là trung điểm của BC. Khi đó ta có GM, GB lần lượt là bán kính đường tròn nội tiếp và bán kính đường tròn ngoại tiếp của tam giác ABC.

Vì ∆ABC là tam giác đều có BG là đường phân giác của góc ABC nên $\widehat{GBM}=\frac{1}{2}\widehat{ABC}=\frac{1}{2}\cdot 60°=30°.$

Vì M là trung điểm của BC nên $BM=\frac{1}{2}BC.$

Xét ∆GBM vuông tại M, ta có

⦁ $GM=GB\cdot \sin \widehat{GBM}=GB\cdot \sin 30°=\frac{1}{2}GB.$

⦁ $GM=BM\cdot \tan \widehat{GBM}=\frac{1}{2}BC\cdot \tan 30°=\frac{1}{2}BC\cdot \frac{\sqrt{3}}{3}=\frac{\sqrt{3}}{6}BC.$

Vậy bán kính đường tròn nội tiếp tam giác ABC bằng một nửa bán kính đường tròn ngoại tiếp tam giác ABC và bằng $\frac{\sqrt{3}}{6}$BC

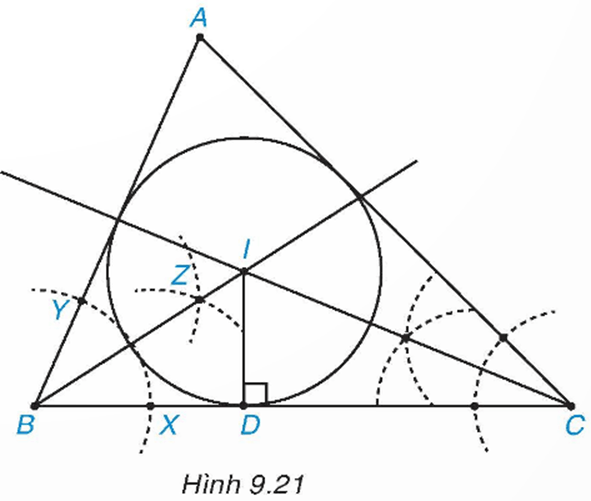
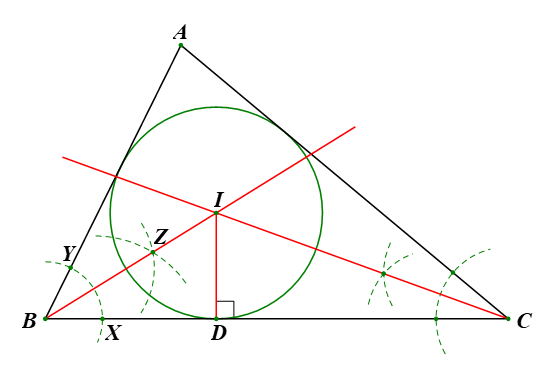
Thực hành trang 75 Toán 9 Tập 2: Vẽ đường tròn nội tiếp của tam giác ABC bằng thước kẻ và compa theo các bước sau:

– Vẽ tia phân giác góc B như sau: Dùng compa vẽ một cung tròn tâm B cắt hai cạnh BC, BA lần lượt tại X và Y. Vẽ hai cung tròn tâm X, Y có cùng bán kính, hai cung này cắt nhau tại một điểm Z khác B. Kẻ tia BZ ta được tia phân giác góc B.

– Tương tự, vẽ tia phân giác góc C, cắt tia BZ tại I.

– Vẽ đường cao ID từ I xuống BC (D thuộc BC). Vẽ đường tròn (I; ID) (H.9.21).

Khi đó đường tròn (I; ID) là đường tròn nội tiếp tam giác ABC cần vẽ.

Lời giải:

HS làm theo hướng dẫn của GV và SGK.

Lời giải bài tập Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác hay khác:

• Giải Toán 9 trang 72

• Giải Toán 9 trang 73

• Giải Toán 9 trang 74

• Giải Toán 9 trang 76