Giải Toán 9 trang 76 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 76 Tập 2 trong Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác Toán 9 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 76.

Giải Toán 9 trang 76 Tập 2 Kết nối tri thức

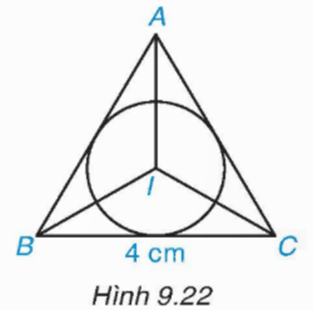
Luyện tập 3 trang 76 Toán 9 Tập 2: Cho tam giác đều ABC (H.9.22).

a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC.

b) Biết rằng BC = 4 cm, hãy tính bán kính r.

Lời giải:

a) Vẽ hai đường phân giác của góc B và C cắt nhau tại I.

Kéo dài AI cắt BC tại D. Khi đó ta vẽ đường tròn (I; ID) thì được đường tròn (I; r) nội tiếp tam giác ABC với ID = r.

b) Vì đường tròn (I; r) nội tiếp tam giác đều ABC có cạnh BC = 4 cm nên có đường tròn này bán kính $r=\frac{\sqrt{3}}{6}BC=\frac{\sqrt{3}}{6}\cdot 4=\frac{2\sqrt{3}}{3}\text{(cm).}$

Vậy $r=\frac{2\sqrt{3}}{3}\text{cm.}$

Bài 9.7 trang 76 Toán 9 Tập 2: Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng tam giác ABC vuông cân tại A và có cạnh bên bằng 2$\sqrt{2}$ cm.

Lời giải:

Vì ∆ABC cân tại A nên AB = AC = 2$\sqrt{2}$ cm.

Áp dụng định lí Pythagore vào ∆ABC vuông tại A, ta có:

BC² = AB² + AC²

Do đó $B{C}^2={\left(2\sqrt{2}\right)}^2+{\left(2\sqrt{2}\right)}^2=16$

Suy ra BC = 4 cm.

Vì O là tâm đường tròn ngoại tiếp tam giác ABC vuông tại A nên bán kính của (O) bẳng một nửa cạnh huyền BC.

Vậy bán kính của (O) là: $R=\frac{BC}{2}=\frac{4}{2}=2\text{(cm)}.$

Bài 9.8 trang 76 Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3 cm. Tính diện tích tam giác ABC.

Lời giải:

Vì tam giác ABC đều nên tâm O của đường tròn ngoại tiếp tam giác là trọng tâm của tam giác đó và bán kính đường tròn ngoại tiếp tam giác là $AO=\frac{\sqrt{3}}{3}BC.$

Theo bài, AO = 3 cm nên $\frac{\sqrt{3}}{3}BC=3$

Suy ra BC = 3$\sqrt{3}$ cm.

Gọi H là giao điểm của AO và BC. Khi đó AH vừa là đường trung trực, vừa là đường trung tuyến, cũng là đường cao của tam giác.

Ta có $AO=\frac{2}{3}AH,$ suy ra $AH=\frac{3}{2}AO=\frac{3}{2}\cdot 3=4,5\text{(cm).}$

Diện tích của tam giác ABC là:

$S=\frac{1}{2}AH\cdot BC=\frac{1}{2}\cdot 4,5\cdot 3\sqrt{3}=\frac{27\sqrt{3}}{4}{\text{(cm}}^2\text{).}$

Vậy diện tích của tam giác ABC là $\frac{27\sqrt{3}}{4}{\text{cm}}^2\text{.}$

Bài 9.9 trang 76 Toán 9 Tập 2: Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng $\widehat{BAH}=\widehat{OAC}.$

Lời giải:

Ta có OA = OB (cùng bằng bán kính đường tròn ngoại tiếp (O) của ∆ABC) nên ∆OAC cân tại O, do đó $\widehat{OAC}=\widehat{OCA}$ (tính chất tam giác cân).

Lại có $\widehat{OAC}+\widehat{OCA}+\widehat{AOC}=180°$ (tổng ba góc của một tam giác)

Suy ra $2\widehat{OAC}+\widehat{AOC}=180°$

Nên $\widehat{OAC}=\frac{180°-\widehat{AOC}}{2}=90°-\frac{\widehat{AOC}}{2}.\left(1\right)$

Gọi K là giao điểm của AH và BC. Khi đó AK là đường cao của tam giac ABC.

Xét ∆ABK vuông tại K có: $\widehat{ABK}+\widehat{BAK}=90°$ (tổng hai góc nhọn của tam giác vuông)

Suy ra $\widehat{BAK}=90°-\widehat{ABK}$ hay $\widehat{BAH}=90°-\widehat{ABC}.\left(2\right)$

Mặt khác, xét đường tròn (O) có $\widehat{ABC},\widehat{AOC}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AC nên $\widehat{ABC}=\frac{1}{2}\widehat{AOC}.\left(3\right)$

Từ (2) và (3) ta có $\widehat{BAH}=90°-\frac{\widehat{AOC}}{2}.\left(4\right)$

Từ (1) và (4) ta có $\widehat{BAH}=\widehat{OAC}.$

Bài 9.10 trang 76 Toán 9 Tập 2: Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng $\widehat{EIF}+\widehat{BAC}=180°.$

Lời giải:

Vì đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F nên IE ⊥ AB và IF ⊥ AC.

Do đó $\widehat{AEI}=\widehat{AFI}=90°.$

Xét tứ giác AEIF có: $\widehat{BAC}+\widehat{AEI}+\widehat{AFI}+\widehat{EIF}=360°$ (tổng các góc của một tứ giác)

Suy ra $\widehat{BAC}+\widehat{EIF}=360°-\widehat{AEI}-\widehat{AFI}=360°-90°-90°=180°.$

Vậy $\widehat{EIF}+\widehat{BAC}=180°.$

Bài 9.11 trang 76 Toán 9 Tập 2: Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1 cm.

Lời giải:

Gọi độ dài các cạnh của tam giác đều ABC là a (cm).

Vì tam giác ABC đều ngoại tiếp đường tròn (I; r) nên ta có $r=\frac{\sqrt{3}}{6}\cdot a$

Theo bài, r = 1 cm nên $1=\frac{\sqrt{3}}{6}\cdot a$

Suy ra $a=2\sqrt{3}\text{(cm).}$

Vậy độ dài các cạnh của tam giác ABC là $2\sqrt{3}\text{cm}.$

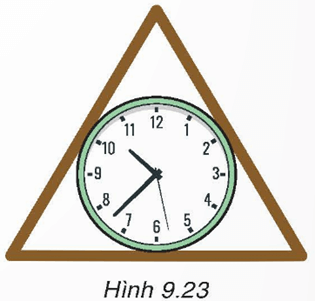
Bài 9.12 trang 76 Toán 9 Tập 2: Người ta muốn làm một khung gỗ hình tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30 cm (H.9.23). Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?

Lời giải:

Gọi độ dài các cạnh phía bên trong của khung gỗ là a (cm).

Bán kính của chiếc đồng hồ hình tròn là: r = 30 : 2 = 15 (cm).

Vì khung gỗ hình tam giác đều để đặt vừa khít chiếc đồng hồ nên đường tròn khung viền của đồng hồ nội tiếp tam giác chứa cạnh của khung gỗ và bán kính đường tròn này là $r=\frac{\sqrt{3}}{6}\cdot a.$

Suy ra $15=\frac{\sqrt{3}}{6}a,$ suy ra $a=30\sqrt{3}\text{(cm).}$

Vậy độ dài cạnh của tam giác (phía bên trong) của khung gỗ là 30$\sqrt{3}$ cm.

Lời giải bài tập Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác hay khác:

• Giải Toán 9 trang 72

• Giải Toán 9 trang 73

• Giải Toán 9 trang 74

• Giải Toán 9 trang 75