Giải Toán 9 trang 95 Tập 2 Kết nối tri thức
Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 95 Tập 2 trong Bài 31: Hình trụ và hình nón Toán 9 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 95.
Giải Toán 9 trang 95 Tập 2 Kết nối tri thức
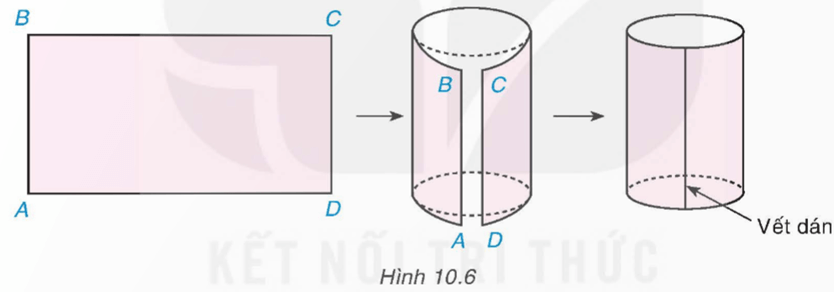
Thực hành 1 trang 95 Toán 9 Tập 2: Chuẩn bị một băng giấy cứng hình chữ nhật ABCD với AB = 8 cm, BC = 15 cm. Cuộn băng giấy lại sao cho hai cạnh AB và DC sát vào nhau như Hình 10.6 (dùng băng keo dán), ta được một hình trụ (không có đáy). Hãy cho biết chiều cao và chu vi đáy của hình trụ đó.
Lời giải:
Chiều cao của hình trụ đó chính là đoạn thẳng AB nên chiều cao bằng 8 cm.
Vì băng giấy được cuộn vào nên ta được hai đáy tạo thành các hình tròn, nên chu vi hình tròn là đoạn thẳng BC. Do đó chu vi đáy của hình trụ bằng 15 cm.
HĐ1 trang 95 Toán 9 Tập 2: Người ta coi diện tích hình chữ nhật ABCD chính là diện tích xung quanh của hình trụ được tạo thành (xem Thực hành 1). Cho hình trụ có chiều cao h = 9 cm và bán kính đáy R = 5 cm. Tính diện tích mặt xung quanh của hình trụ.
Lời giải:
Hình chữ nhật ABCD có một cạnh bằng chu vi hình tròn đáy, cạnh còn lại bằng chiều cao của hình trụ.
Nên ta có một cạnh của hình chữ nhật bằng 9 cm.
Cạnh còn lại của hình chữ nhật (hay chu vi hình tròn đáy) là:
2π . R = 2π . 5 = 10π (cm).
Diện tích hình chữ nhật ABCD là:
10π . 9 = 90π (cm2).
Vậy diện tích xung quanh của hình trụ là 90π cm2.
HĐ2 trang 95 Toán 9 Tập 2: Hãy nhắc lại công thức tính thể tích của hình lăng trụ đứng tam giác (hoặc hình lăng trụ đứng tứ giác) có diện tích đáy S và chiều cao h.
Lời giải:
Thể tích của hình lăng trụ đứng tam giác (hoặc hình lăng trụ đứng tứ giác) có diện tích đáy S và chiều cao h là: V = S . h.
Lời giải bài tập Toán 9 Bài 31: Hình trụ và hình nón hay khác: