Bài tập về quy tắc cộng nâng cao cực hay có lời giải - Toán lớp 11
Bài tập về quy tắc cộng nâng cao cực hay có lời giải
Với Bài tập về quy tắc cộng nâng cao cực hay có lời giải Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập quy tắc cộng nâng cao từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải
Định nghĩa : Giả sử một công việc được thực hiện theo phương án A hoặc phương án B. Có n cách thực hiện phương án A và m cách thực hiện phương án B. Khi đó công việc có thể được bởi n + m cách.
Mở rộng : Giả sử một công việc có thể được thực hiện theo một trong k phương án A1; A2... :Ak. Có n1 cách thực hiện phương án A1; n2 cách thực hiện phương án A2; ...; có nk cách thực hiện phương án Ak.Khi đó, công việc có thể được thực hiện bởi n1 + n2 +...+ nk cách.
Chú ý :
+ S ố phần tử của tập hợp hữu hạn X được kí hiệu là |X| ( hoặc n( X)).
+ Quy tắc cộng có thể được phát biểu dưới dạng sau:
Nếu A và B là hai tập hợp hữu hạn không giao nhau thì số phần tử của A∪B bằng số phần tử của A cộng với số phần tử của B; tức là:
|A∪B|= |A|+ |B|
+ Quy tắc cộng cho ta tính số phần tử của hợp hai tập hợp hữu hạn không giao nhau. Tuy nhiên, trong nhiều bài toán tổ hợp; chúng ta phải tính số phần tử của hợp hai tập hợp hữu hạn A và B có giao khác ∅. Trong trường hợp này; khi cộng số phần tử của A với số phần tử của B; thì số phần tử của A∩B được tính 2 lần. Từ đó;ta có quy tắc cộng mở rộng sau đây:
Cho hai tập hợp hữu hạn bất kì A và B. Khi đó; số phần tử của A∪ B bằng số phần tử A cộng với số phần tử của B rồi trừ đi số phần tử của A∩B; tức là:
|A∪B|= |A|+ |B|- |A∩B|
⇒ Mở rộng: với ba tập hợp hữu hạn A; B và C bất kì ta có:
|A∪B∪C|= |A|+ |B|+ |C|- |A∩B|- |B∩C|- |A∩C|+ |A∩B∩C|
B. Ví dụ minh họa
Ví dụ 1 : Một khối 11 của trường THPT A có: 160 học sinh tham gia câu lạc bộ tin học; 120 học sinh tham gia câu lạc bộ tiếng anh. Có 70 học sinh tham gia cả hai câu lạc bộ. Hỏi có bao nhiêu học sinh khối 11 tham gia hai câu lạc bộ đó ( tin học hoặc tiếng anh) ?
A.190 B.210 C. 230 D. 250
Hướng dẫn giải :
Đáp án : B
Gọi tập hợp học sinh khối 11 của trường THPT A tham gia câu lạc bộ tin học và câu lạc bộ tiếng anh lần lượt là A và B.
Khi đó tập hợp học sinh khối 11 của trường đó tham gia câu lạc bộ ( tin học hoặc tiếng anh) là: A∪B.
Theo đề bài ta có: |A|=160; |B|=120; |A∩B|=70.
Theo quy tắc cộng mở rộng; số học sinh khối 11 tham gia câu lạc bộ ( tin học hoặc tiếng anh) là : |A∪B|= |A|+ |B|- |A∩B| = 160+ 120 – 70= 210 ( học sinh )
Ví dụ 2 : Lớp 10 A có 26 học sinh giỏi toán và 21 học sinh giỏi văn. Biết rằng có 10 học sinh giỏi cả 2 môn. Hỏi lớp 10 A có bao nhiêu học sinh giỏi toán hoặc văn?
A. 37 B. 25 B. 35 D. 29
Hướng dẫn giải :
Đáp án : A
Gọi tập hợp học sinh lớp 10A giỏi toán và văn lần lượt là A và B.
Khi đó; tập hợp học sinh của lớp đó giỏi toán hoặc văn là: A∪B.
Theo đề bài ta có: |A|=26; |B|=21; |A∩B|=10.
Theo quy tắc cộng mở rộng; số học sinh giỏi toán hoặc văn là :
|A∪B|= |A|+ |B|- |A∩B| = 26+ 21 – 10 = 37 học sinh.
Ví dụ 3 : Lớp 12 A có 30 học sinh học giỏi toán; 24 học sinh học giỏi tiếng anh và có 12 học sinh học giỏi cả hai môn.Biết rằng có 7 bạn không học giỏi môn nào trong hai môn trên. Hỏi lớp đó có bao nhiêu học sinh?
A. 49 B. 42 C. 45 D.47
Hướng dẫn giải :
Đáp án : A
Gọi tập hợp học sinh lớp 12 A giỏi toán và anh lần lượt là A và B.
Khi đó; tập hợp các học sinh giỏi ít nhất một môn toán hoặc anh là: A∪B
Theo đề bài ta có: |A|=30; |B|=24; |A∩B|=12.
⇒ Số học sinh giỏi ít nhất một môn toán hoặc anh là:
|A∪B|= |A|+ |B|- |A∩B| = 30+ 24 – 12 = 42 học sinh.
⇒ Lớp đó có số học sinh là:
42+ 7= 49 học sinh
Ví dụ 4 : Cho tập hợp A có 21 phần tử; tập B có 12 phần tử.Biết rằng có 7 phần tử vừa thuộc A vừa thuộc B. Hỏi hai tập A và B có tất cả bao nhiêu phần tử?
A. 27 B. 31 C. 25 D. 26
Hướng dẫn giải :
Đáp án : D
Theo giả thiết ta có:|A|=21;|B|=12; |A∩B|=7
Áp dụng quy tắc cộng mở rộng; hai tập A và B có tất cả số phần tử là:
|A∪B|= |A|+ |B|- |A∩B|=21+12-7=26
Ví dụ 5 : Trong khoa toán – tin của trường đại học sư phạm Hà Nội có : 110 bạn tham gia câu lạc bộ tình nguyện; 80 bạn tham gia câu lạc bộ thể dục thể thao và có 20 bạn tham gia cả hai câu lạc bộ. Hỏi khoa toán tin có bao nhiêu sinh viên; biết rằng có 500 học sinh không tham gia câu lạc bộ nào cả?
A. 610 B.650 C. 670 D. 710
Hướng dẫn giải :
Đáp án : C
+ Gọi tập hợp các sinh viên tham gia câu lạc bộ tình nguyện và câu lạc bộ thể dục thể thao lần lượt là A và B.
Theo giả thiết ta có: |A|=110;|B|=80; |A∩B|=20
+ Khi đó tập hợp các sinh viên của khoa đó tham gia câu lạc bộ là; A∪B
Ta có: |A∪B|= |A|+ |B|- |A∩B|=110+80-20=170 sinh viên
⇒ Số sinh viên của khoa toán tin là: 170+ 500= 670 sinh viên

Ví dụ 6 : Có bao nhiêu số nguyên dương không lớn hơn 1000 mà chia hết cho 4 hoặc cho 7?
A. 392 số B. 357 số C. 410 số D. 250 số
Hướng dẫn giải :
Đáp án : B
Chú ý không tính số 0, ta xét các số dạng 4k ( chia hết cho 4); 7l ( chia hết cho 7) và 28 p( chia hết cho cả 4 và 7).
Ta có :
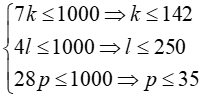
Suy ra: Có 142 số chia hết cho 7, 250 số chia hết cho 4, 35 số đồng thời chia hết cho 4 và 7.
Vậy ta có 142 + 250 – 35 = 357 số cần tìm.
Ví dụ 7 : Một lớp học có 30 học sinh, trong đó có 18 em giỏi Toán, 14 em giỏi văn và 10 em không giỏi môn nào. Số tất cả các em giỏi cả văn lẫn toán là:
A. 20 B. 12 C. 24 D. 48
Hướng dẫn giải :
Đáp án : B
Số học sinh giỏi ít nhất 1 môn là: 30 – 10 = 20
Số học sinh giỏi cả văn lẫn toán là: 18 + 14 – 20 = 12.
Ví dụ 8 : Lớp 10A2 có: 25 học sinh giỏi toán; 15 học sinh giỏi văn; 22 học sinh giỏi tiếng anh. Biết rằng có 10 học sinh học giỏi hai môn toán và văn; 8 học sinh giỏi 2 môn văn và anh; 9 học sinh giỏi toán và anh; 5 học sinh học giỏi cả ba môn. Hỏi có bao nhiêu học sinh giỏi ít nhất một trong ba môn?
A. 35 B .45 C. 40 D. 37
Hướng dẫn giải :
Đáp án : C
Gọi A là tập hợp các bạn giỏi toán.
B là tập hợp các bạn giỏi văn và C là tập hợp các bạn giỏi anh .
⇒ A∪B∪C: là tập hợp các học sinh giỏi ít nhất một trong ba môn.
Theo đầu bài ta có: |A|=25; |B|=15; |C|=22;|A∩B|=10;
|A∩C|=9; |B∩C|=8; |A∩B∩C|=5
Theo quy tắc cộng mở rộng ta có:
|A∪B∪C|= |A|+ |B|+ |C|-|A∩B|- |A∩C|- |B∩C|+ |A∩B∩C|= 25+ 15+ 22-10- 9- 8 + 5 = 40
C. Bài tập trắc nghiệm
Câu 1 : Một lớp có 25 học sinh khá môn Toán, 24 học sinh khá môn Ngữ Văn, 10 học sinh khá cả môn Toán và môn Ngữ Văn và 3 học sinh không khá cả Toán và Ngữ Văn. Hỏi lớp học đó có bao nhiêu học sinh?
A. 39 B. 42 C. 62 D. 52
Lời giải:
Đáp án : B
Gọi A là tập các học sinh khá môn Toán và B là tập các học sinh khá môn Ngữ Văn
Theo đề ta có:|A| = 25;|B| = 24;|A∩B|=10
Theo quy tắc tính số phần tử của hợp hai tập hợp hữu hạn bất kì ta có:|A∪B|= |A|+|B|-|A∩B|= 25 + 24 - 10 = 39
Vậy lớp học có: 39+ 3= 42 học sinh.
Câu 2 : Trong kì thi tuyển nhân viên chuyên môn cho công ty X, ở khối A có 51 thí sinh đạt điểm giỏi môn Toán, 73 thí sinh đạt điểm giỏi môn Vật lí, 73 thí sinh đạt điểm giỏi môn Hóa học, 32 thí sinh đạt điểm giỏi cả hai môn Toán và Vật lí, 45 thí sinh đạt điểm giỏi cả hai môn Vật lí và Hóa học 21 thí sinh đạt điểm giỏi cả hai môn Toán và Hóa học, 10 thí sinh đạt điểm giỏi cả ba môn Toán, Vật lí và Hóa học. Có 767 thí sinh mà cả ba môn đều không có điểm giỏi. Hỏi có bao nhiêu thí sinh tham dự tuyển nhân viên chuyên môn cho công ty?
A. 867 B. 776 C. 576 D. 792
Lời giải:
Đáp án : A
Kí hiệu A; B; C tương ứng là tập hợp các thí sinh đạt điểm giỏi ở ít nhất một trong ba môn là Toán, Vật lý, Hóa học.
|A|=51; |B|=73; |C|=64; |A∩B|=32; |B∩C|=45; |A∩C|=21; |A∩B∩C|=10
Lúc này ta có A∪B∪C là tập hợp các học sinh đạt điểm giỏi ở ít nhất một trong ba môn là Toán, Vật lý, Hóa học. Ta có:
|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|B∩C|-|A∩C|+|A∩B∩C| = 51+73+64-32-45-21+10=100.
Vậy số thí sinh dự tuyển vào công ty là: 100+ 767= 867
Câu 3 : Người ta phỏng vấn 100 người về ba bộ phim A; B; C đang chiếu thì thu được kết quả như sau:
Bộ phim A: có 28 người đã xem.
Bộ phim B: có 26 người đã xem.
Bộ phim C: có 14 người đã xem.
Có 8 người đã xem hai bộ phim A và B
Có 4 người đã xem hai bộ phim B và C
Có 3 người đã xem hai bộ phim A và C
Có 2 người đã xem cả ba bộ phim A, B và C.
Số người không xem bất cứ phim nào trong cả ba bộ phim A;B;C là:
A. 55 B. 45 C. 32 D. 51
Lời giải:
Đáp án : B
Theo quy tắc tính số phần tử của ba tập hợp hữu hạn bất kì, ta có số người xem ít nhất một bộ phim là :
28+26 + 14- 8-4 – 3+ 2= 55 người.
Vậy số người không xem bất cứ bộ phim nào là 100-55 =45 người

Câu 4 : Lớp 12A có 20 bạn thích nhóm nhạc bigbang; 15 bạn thích nhóm nhạc HKT và 5 bạn thích cả 2 nhóm nhạc. Hỏi lớp 12 A có bao nhiêu học sinh; biết rằng có 10 bạn không thích nhóm nhạc nào cả ?
A. 35 B. 42 C. 38 D. 40
Lời giải:
Đáp án : D
Gọi A là tập hợp các bạn thích nhóm nhạc bigbang. B là tập hợp các bạn thích nhóm nhạc HKT.
⇒ A∪B là tập hợp các bạn thích ít nhất 1 nhóm nhạc.
Ta có: |A|=20 ; |B|=15 ; |A∩B|=5.
⇒ Số bạn thích ít nhất 1 nhóm nhạc là:
|A∪B|= |A|+ |B|- |A∩B|=20+15-5=30
Lớp 12 A có tất cả số học sinh là: 30+ 10 = 40 học sinh
Câu 5 : Trong một lần điều tra về ngành phát triển du lịch của một công ty thu được kết quả sau:
Có 300 người từng đi du lịch Đà Nẵng và Vịnh Hạ Long.
Có 400 người đi du lịch Đà nẵng; chưa đi Vịnh Hạ Long.
Có 350 người đi du lịch Vịnh Hạ Long; chưa đi Đà Nẵng.
Có 50 người chưa đi du lịch.
Hỏi công ty đó có bao nhiêu người?
A. 500 B.600 C. 450 D. 550
Lời giải:
Đáp án : A
Gọi A là tập hợp những người đi du lịch Đà nẵng.
B là tập hợp những người đi du lịch Vịnh Hạ Long
⇒ A∪B là tập hợp những người đã đi du lịch Đà Nẵng hoặc Vịnh Hạ Long.
Theo giả thiết ta có: |A|= 400; |B|=350.; |A∩B|=300
Theo quy tắc cộng mở rộng; số người từng đi du lịch ít nhất 1 lần là:
|A∪B|= |A|+ |B|- |A∩B|=400+350-300=450
⇒ Công ty có tất cả:450 + 50= 500 người.
Câu 6 : Trong một buổi kiểm tra đồ dùng học tập của lớp 5A; cô giáo chủ nhiệm thu được kết quả như sau:
Có 15 bạn thiếu bút màu; có 10 bạn thiếu giấy dán và 7 bạn thiếu cả bút màu; giấy dán. Hỏi lớp 5A có bao nhiêu học sinh, biết rằng có 25 học sinh đầy đủ dụng cụ học tập?
A.40 B.38 C . 43 D .45
Lời giải:
Đáp án : C
Gọi A là tập hợp các học sinh thiếu bút màu.
Gọi B là tập hợp các học sinh thiếu giấy dán.
⇒ A∪B: tập hợp các bạn thiếu bút màu hoặc giấy dán.
Theo đề bài ta có: |A|=15; |B|= 10; |A∩B|=7
Theo quy tắc cộng mở rộng ta có:
|A∪B|=15+10-7=18
Lớp 5A có tất cả số học sinh là: 18+ 25= 43 học sinh
Câu 7 : Trong một nhóm văn nghệ có 10 bạn thích nhạc trẻ; 12 bạn thích nhạc vàng và 18 bạn thích nhạc trẻ hoặc nhạc vàng. Hỏi có bao nhiêu bạn thích cả hai thể loại nhạc?
A. 3 B .4 C .5 D . 6
Lời giải:
Đáp án : C
Gọi A là tập hợp các bạn thích nhạc trẻ.
Gọi B là tập hợp các bạn thích nhạc vàng.
⇒ A∪B :tập hợp các bạn thích nhạc trẻ hoặc nhạc vàng; A∩B là tập hợp các bạn thích cả hai thể loại nhạc.
Theo đầu bài ta có:
|A|=10 ; |B|=12; |A∪B|=18
Theo quy tắc cộng mở rộng ta có:
|A∪B|= |A|+ |B|- |A∩B|
⇔ 18= 10+ 12- |A∩B| nên |A∩B| = 4
Vậy có 4 bạn thích cả hai loại nhạc.
Câu 8 : Có bao nhiêu số nguyên dương không vượt quá 1000 mà chia hết cho 3 hoặc chia hết cho 5?
A. 531 số B. 533 số C. 332 số D. 467 số
Lời giải:
Đáp án : D
+ Số chia hết cho 3 có dạng 3a.
Ta có: 0< 3a ≤ 1000 ⇔ 0< a < 333,3 nên có 333 số thỏa mãn
+ Số chia hết cho 5 có dạng 5b.
Ta có 0< 5b ≤1000 nên 0<b≤200 nên có 200 số thỏa mãn
+ Số chia hết cho cả 3 và 5 có dạng 15c.
Ta có 0< 15c ≤1000 nên 0<c≤66,6 nên có 66 số thỏa mãn
+ Theo quy tắc cộng mở rộng; số các số thỏa mãn đề bài là:
333+ 200 – 66= 467

