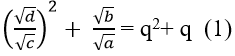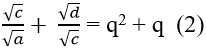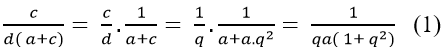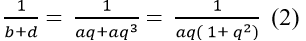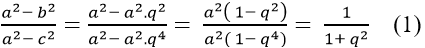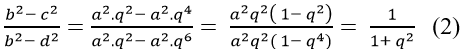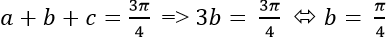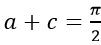Cách chứng minh đẳng thức dựa vào tính chất của cấp số nhân cực hay - Toán lớp 11

---

Cách chứng minh đẳng thức dựa vào tính chất của cấp số nhân cực hay

Với Cách chứng minh đẳng thức dựa vào tính chất của cấp số nhân cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập chứng minh đẳng thức dựa vào tính chất của cấp số nhân từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

* Cho (un) là cấp số nhân; có số hạng đầu là u1 và công bội q. Theo tính chất của cấp số nhân ta có: u_n² = u_n-1.u_n+1 với n ≥ 2.

* Để chứng minh ba số a,b,c theo thứ tự lập thành cấp số nhân ta cần chứng minh: ac = b².

B. Ví dụ minh họa

Ví dụ 1: Cho a, b, c là ba số hạng liên tiếp của một cấp số nhân. Chứng minh: (ab+ bc+ ca)³ = abc( a+ b+ c)³

Hướng dẫn giải:

Vì a, b, c là ba số hạng liên tiếp của một cấp số nhân, nên có ac= b².

Ta có:

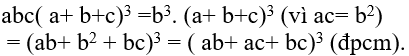
Ví dụ 2: Cho a,b,c là ba số hạng liên tiếp của một cấp số nhân. Chứng minh : (a² + b²).(b² + c²) = (ab + bc)²

Hướng dẫn giải:

Ta có:

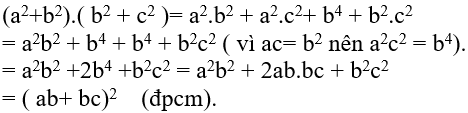
Ví dụ 3: Cho 3 số a, b và c theo thứ tự lập thành cấp số nhân với công bội q≠0 và a ≠ 0. Chứng minh: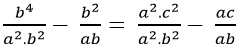

Hướng dẫn giải:

Do 3 số a, b và c theo thứ tự lập thành cấp số nhân nên ta có:

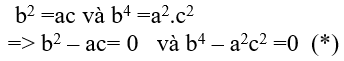
Ta có:

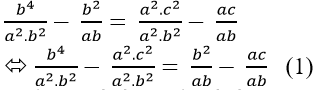
Lại có: 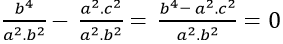(do (*) ( 2)

Và 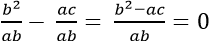(do (*)) (3)

Từ (1),(2) và (3) ta có điều phải chứng minh.

Ví dụ 4: Cho bốn số a,b, c và d theo thứ tự lập thành cấp số nhân. Chứng minh: ac + 2ad + bd = (b+c)²

Hướng dẫn giải:

* Do bốn số a,b,c và d theo thứ tự lập thành cấp số nhân nên ta có:

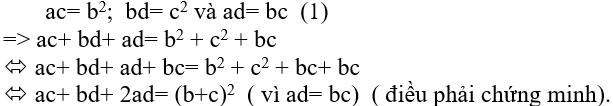
Ví dụ 5: Cho bốn số dương a ,b,c và d thỏa mãn √a; √b; √c và √d theo thứ tự lập thành cấp số nhân. Chứng minh: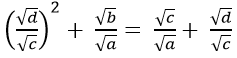

Hướng dẫn giải:

Gọi 4 số √a; √b; √c và √d theo thứ tự lập thành cấp số nhân với công bội q. Ta có:

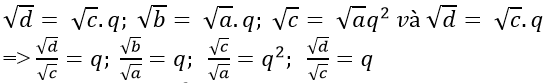
Do đó; ta có:

Và

Từ (1) và (2) suy ra: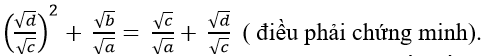

Ví dụ 6: Cho bốn số dương a, b, c và d theo thứ thự lập thành cấp số nhân. Chứng minh: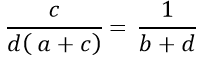

Hướng dẫn giải:

Gọi 4 số a,b, c, và d theo thứ tự lập thành cấp số nhân có công bội q. Ta có:

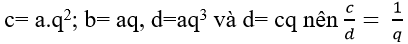
Khi đó;

Và

Từ (1) và (2) suy ra: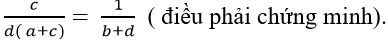

Ví dụ 7: Cho bốn số dương phân biệt a, b, c và d theo thứ tự lập thành cấp số nhân. Chứng minh: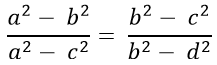

Hướng dẫn giải:

* Do bốn số a, b, c và d theo thứ tự lập thành cấp số nhân công bội q nên

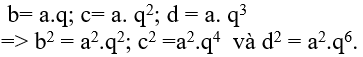
* Ta có:

( chú ý bốn số đã cho là phân biệt nên q ≠ 1)

* Lại có :

Từ (1) và (2) ta có: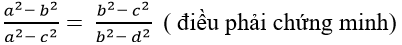

C. Bài tập trắc nghiệm

Câu 1: Cho a,b,c là ba số hạng liên tiếp của cấp số nhân .Chứng minh : (a + b +c). (a - b + c) = a² + b² + c²

Lời giải:

*Ta có a, b và c theo thứ tự lập thành cấp số nhân nên ta có: b² = ac

* Xét:

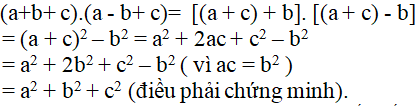
Câu 2: Cho a, b, c và d theo thứ tự lập thành cấp số nhân. Chứng minh: (b-c)² + (c-a)² + ( d- b)² + ( a- d)² = (a-d)²

Lời giải:

Vì a,b,c và d theo thứ tự lập thành cấp số nhân nên ta có:

a.d= bc; ac = b² và bd= c²

Ta có:

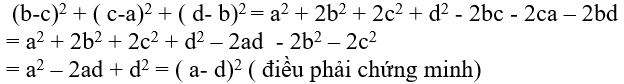
Câu 3: Cho a, b và c theo thứ tự lập thành cấp số nhân. Chứng minh: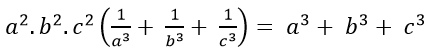

Lời giải:

* Do a,b và c theo thứ tự lập thành cấp số nhân nên ta có:

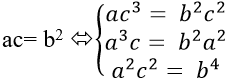
* Ta có:

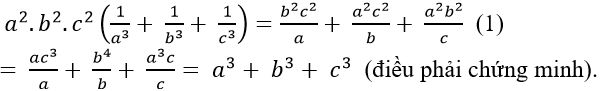
Câu 4: Cho ba số dương a,b,c lập thành cấp số nhân. Chứng minh: cũng lập thành cấp số nhân.

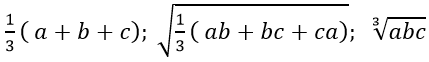
Lời giải:

* Ta có a, b và c theo thứ tự lập thành cấp số nhân nên: ac= b² *Ta phải chứng minh:

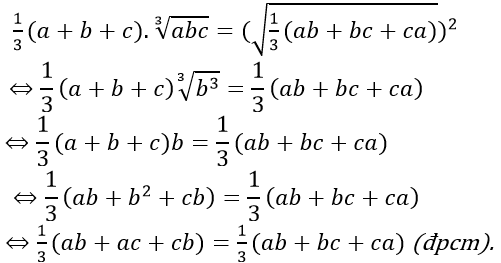
Câu 5: Cho (u_n) là cấp số nhân và các số nguyên dương m; k ( m < k). Chứng minh: u_k-m . u_k+m = u_k²

Lời giải:

Ta có :

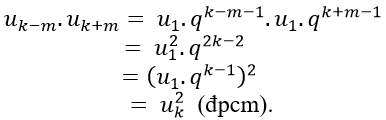
Câu 6: Cho 3 số a,b, c là 3 số hạng liên tiếp của cấp số nhân. Chứng minh: (a²+ b²). (b² + c²)= ( ab+ bc)²

Lời giải:

Do 3 số a, b, c là 3 số hạng liên tiếp của cấp số nhân. Gọi q là công bội của cấp số nhân ta có: b= aq và c= aq²

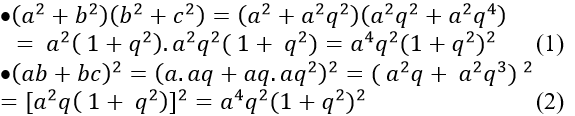
• Từ (1) và (2) ta suy ra 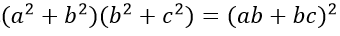.( đpcm)

Câu 7: Cho a, b, c là cấp số cộng thỏa mãn: 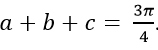. Chứng minh tan a; tanb và tan c theo thứ tự đó lập thành cấp số nhân.

Lời giải:

* Ta có a, b và c theo thứ tự lập thành cấp số cộng nên a + c= 2b.

Lại có:

Suy ra

* Ta có

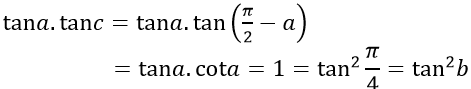
Vậy tan a. tan c= tan²

=> tana; tanb; tanc theo thứ tự đó lập thành cấp số nhân.