Bài tập trắc nghiệm lý thuyết đường thẳng vuông góc với mặt phẳng cực hay - Toán lớp 11
Bài tập trắc nghiệm lý thuyết đường thẳng vuông góc với mặt phẳng cực hay
Với Bài tập trắc nghiệm lý thuyết đường thẳng vuông góc với mặt phẳng cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập đường thẳng vuông góc với mặt phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải
1. Định nghĩa
Một đường thẳng gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
d ⊥ (P) ⇔ d ⊥ a, ∀a ⊂ (P)
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
Định lí: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì đường thẳng d vuông góc với mặt phẳng (P).
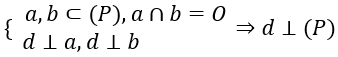
3. Tính chất
Tính chất 1: Có duy nhất một mặt phẳng (P) đi qua một điểm O cho trước và vuông góc với đường thẳng a cho trước.
Tính chất 2: Có duy nhất một đường thẳng Δ đi qua một điểm O cho trước và vuông góc với một mặt phẳng (P) cho trước.
* Mặt phẳng trung trực của một đoạn thẳng là mặt phẳng vuông góc với đoạn thẳng tại trung điểm của nó.
* Mặt phẳng trung trực của đoạn thẳng là tập hợp các điểm cách đều hai đầu mút của đoạn thẳng đó.
4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.
* Tính chất 3:
a. Mặt phẳng nào vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng còn lại
b. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
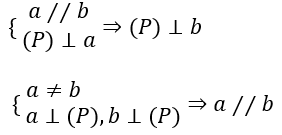
* Tính chất 4:
a. Đường thẳng nào vuông góc với một trong hai mặt phẳng song song thì cũng vuông góc với mặt phẳng còn lại.
b. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau
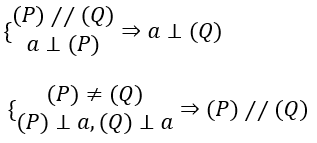
* Tính chất 5
a. Cho đường thẳng a mặt phẳng (P) song song với nhau. Đường thẳng nào vuông góc với (P) thì cũng vuông góc với a.
b. Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng thì chúng song song với nhau.
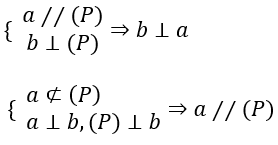
4. Định lí ba đường vuông góc
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng b nằm trong (P). Khi đó, điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a’ của a trên (P)
Cho a không vuông góc (P), b ⊂ (P), a' là hình chiếu của a trên (P). Khi đó b ⊥ a, b ⊥ a'
5. Góc giữa đường thẳng và mặt phẳng

B. Ví dụ minh họa
Ví dụ 1: Cho hai đường thẳng phân biệt a; b và mặt phẳng (P), trong đó a ⊥ (P). Mệnh đề nào sau đây là sai?
A. Nếu b ⊥ (P) thì b // a
B. Nếu b // (P) thì b ⊥ a
C. Nếu b // a thì b ⊥ (P)
D. Nếu b ⊥ a thì b // (P)
Hướng dẫn giải:
Chọn D
Ví dụ cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng đáy. Khi đó; SA ⊥ AB nhưng AB không song song với (ABCD)
Ví dụ 2: Trong không gian cho đường thẳng Δ và điểm O . Qua O có mấy đường thẳng vuông góc với Δ cho trước?
A. 1 B. 2 C. 3 D. Vô số.
Hướng dẫn giải
Chọn D
Qua điểm O có thể dựng vô số đường thẳng vuông góc với Δ, các đường thẳng đó cùng nằm trong một mặt phẳng vuông góc với Δ.
Ví dụ 3: Mệnh đề nào sau đây có thể sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song.
D. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường thẳng thì song song nhau.
Hướng dẫn giải
Chọn C
Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song chỉ đúng khi ba đường thẳng đó đồng phẳng
Ví dụ 4: Khẳng định nào sau đây sai?
A. Nếu đường thẳng d ⊥ (α) thì d vuông góc với hai đường thẳng trong (α)
B. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong (α) thì d ⊥ (α)
C. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong (α) thì d vuông góc với bất kì đường thẳng nào nằm trong (α) .
D. Nếu d ⊥ (α) và đường thẳng a // (α) thì d ⊥ a
Hướng dẫn giải
Chọn B.
Đường thẳng d vuông góc với hai đường thẳng nằm trong (α) thì d ⊥ (α) chỉ đúng khi hai đường thẳng đó cắt nhau.

Ví dụ 5: Trong không gian tập hợp các điểm M cách đều hai điểm cố định A và B là
A. Mặt phẳng trung trực của đoạn thẳng AB
B. Đường trung trực của đoạn thẳng AB
C. Mặt phẳng vuông góc với AB tại A
D. Đường thẳng qua A và vuông góc với AB
Hướng dẫn giải
Chọn A
Theo định nghĩa mặt phẳng trung trực
Ví dụ 6: Trong không gian cho đường thẳng Δ và điểm O . Qua O có bao nhiêu đường thẳng vuông góc với Δ cho trước?
A. Vô số B. 2 C. 3 D. 1
Hướng dẫn giải
Chọn A.
Tập hợp các đường thẳng đó là một mặt phẳng qua O và vuông góc với Δ
Ví dụ 7: Qua điểm O cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng Δ cho trước?
A. 1 B. Vô số C. 3 D. 2
Hướng dẫn giải
Theo tiên đề qua điểm O cho trước có duy nhất một mặt phẳng vuông góc với đường thẳng Δ
Chọn đáp án A.
Ví dụ 8: Trong không gian cho đường thẳng Δ không nằm trong mp(P) , đường thẳng Δ được gọi là vuông góc với mp (P) nếu:
A. vuông góc với hai đường thẳng phân biệt nằm trong mp (P)
B. vuông góc với đường thẳng a mà a song song với mp (P)
C. vuông góc với đường thẳng a nằm trong mp (P)
D. vuông góc với mọi đường thẳng nằm trong mp (P)
Hướng dẫn giải
Đường thẳng Δ được gọi là vuông góc với mặt phẳng (P) nếu Δ vuông góc với mọi đường thẳng trong mặt phẳng (P). (định nghĩa đường thẳng vuông góc với mặt phẳng).
Vậy đáp án D đúng.
Ví dụ 9: Cho a, b, c là các đường thẳng trong không gian. Tìm mệnh đề sai trong các mệnh đề sau.
A. Nếu a ⊥ b và b ⊥ c thì a // c
B. Nếu a vuông góc với mặt phẳng (α) và b // (α) thì a ⊥ b
C. Nếu a // b và b ⊥ c thì c ⊥ a
D. Nếu a ⊥ b , b ⊥ c và a cắt c thì b vuông góc với mặt phẳng (a; c)
Hướng dẫn giải
Nếu 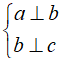
Chọn A.
Ví dụ 10: Trong các mệnh đề sau, mệnh đề nào sai?
A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước.
C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Hướng dẫn giải
Qua một điểm cho trước có thể kẻ được vô số mặt phẳng vuông góc với mặt phẳng cho trước.
Vậy chọn đáp án D.

C. Bài tập vận dụng
Câu 1: Cho hai đường thẳng a, b và mp (P) . Chỉ ra mệnh đề đúng trong các mệnh đề sau:
A. Nếu a // (P) và b ⊥ a thì b // (P) .
B. Nếu a // (P) và b ⊥ (P) thì a ⊥ b .
C. Nếu a // (P) và b ⊥ a thì b ⊥ (P).
D. Nếu a ⊥ (P) và b ⊥ a thì b // (P).
Lời giải:
Câu A sai vì b có thể vuông góc với a .
Câu B đúng bởi a // (P) ⇒ ∃a' ⊂ (P) sao cho a // a’, b ⊥ (P) ⇒ b ⊥ a'. Khi đó a ⊥ b .
Câu C sai vì b có thể nằm trong (P)
Câu D sai vì b có thể nằm trong (P)
Vậy chọn B.
Câu 2: Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Hai đường thẳng chéo nhau và vuông góc với nhau. Khi đó có một và chỉ một mp chứa đường thẳng này và vuông góc với đường thẳng kia.
B. Qua một điểm O cho trước có một mặt phẳng duy nhất vuông góc với một đường thẳng Δ cho trước.
C. Qua một điểm O cho trước có một và chỉ một đường thẳng vuông góc với một đường thẳng cho trước.
D. Qua một điểm O cho trước có một và chỉ một đường thẳng vuông góc với một mặt phẳng cho trước.
Lời giải:
Chọn C
Cho trước đường thẳng d và điểm O thì tâp hợp các đường thẳng qua O và vuông góc với d là mặt phẳng (P) qua O và vuông góc với d. Khi đó, trong mp (P) mỗi đường thẳng qua O sẽ là một đường thẳng vuông góc với d.
Câu 3: Tập hợp các điểm cách đều các đỉnh của một tam giác là đường thẳng vuông góc với mặt phẳng chứa tam giác đó và đi qua:
A. Tâm đường tròn ngoại tiếp tam giác đó.
B. Trọng tâm tam giác đó.
C. Tâm đường tròn nội tiếp tam giác đó.
D. Trực tâm tam giác đó.
Lời giải:
Tập hợp các điểm cách đều các đỉnh của một tam giác là đường thẳng vuông góc với mặt phẳng chứa tam giác đó và đi qua tâm đường trong ngoại tiếp tam giác đó. ( tâm đường tròn ngoại tiếp tam giác là điểm cách đều ba đỉnh của tam giác) . Đường thẳng nói trên được gọi là trục đường tròn ngoại tiếp tam giác.
Chọn A.
Câu 4: Chọn mệnh đề đúng trong các mặt phẳng sau:
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
C. Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song.
D. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
Lời giải:
Đáp án A sai vì hai đường thẳng đó có thể chéo nhau.
Đáp án B sai vì hai mặt phẳng đó có thể cắt nhau.
Đáp án C sai vì hai đường thẳng đó có thể trùng nhau.
Chọn đáp án D.
Câu 5: Chỉ ra mệnh đề sai trong các mệnh đề sau:
A. Cho hai đường thẳng vuông góc với nhau, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
B. Hai đường thẳng phân biệt cùng vuông góc với một mp thì song song với nhau.
C. Cho hai mp song song, đường thẳng nào vuông góc với mặt mp này thì cũng vuông góc với mp kia.
D. Cho hai đường thẳng song song, mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Lời giải:
Chọn A
Ví dụ cho hình chóp S.ABCD có SA vuông góc với mp(ABCD). Ta có AB và SA vuông góc với nhau; SA vuông góc với mp(ABCD) nhưng AB không vuông góc với mp(ABCD).

Câu 6: Trong các mệnh đề sau, mệnh đề nào sai?
A. Nếu đường thẳng a song song với mặt phẳng (P) và đường thẳng b vuông góc với a thì b vuông góc với mặt phẳng (P).
B. Nếu đường thẳng a song song với đường thẳng b và b song song với mặt phẳng (P) thì a song song hoặc nằm trên mặt phẳng (P) .
C. Nếu đường thẳng a song song với mặt phẳng (P) và đường thẳng b vuông góc với mặt phẳng (P) thì a vuông góc với b .
D. Một đường thẳng vuông góc với hai đường thẳng cắt nhau trong một mặt phẳng thì nó vuông góc với mặt phẳng đó.
Lời giải:
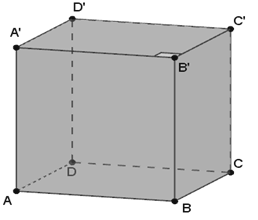
Giả sử xét hình lập phương ABCD.A'B'C'D' như hình vẽ có
Chọn đáp án A.
Câu 7: Cho hình chóp S.ABC có SA = SB = SC và tam giác ABC vuông tại B . Vẽ SH ⊥ (ABC), H ∈ (ABC). Khẳng định nào sau đây đúng?
A. H trùng với trọng tâm tam giác ABC.
B. H trùng với trực tâm tam giác ABC.
C. H trùng với trung điểm của AC
D. H trùng với trung điểm của BC
Lời giải:
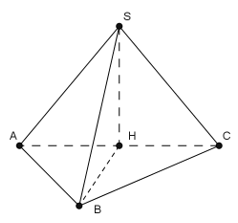
Chọn C
Do SA = SB = SC và SH vuông góc với mp(ABC) nên HA = HB = HC
Suy ra H là tâm đường tròn ngoại tiếp tam giác ABC.
Mà tam giác ABC vuông tại B nên H là trung điểm của AC
(SH được gọi là trục đường tròn ngoại tiếp tam giác ABC)
Câu 8: Cho hình chóp S. ABCD có các cạnh bên bằng nhau SA= SB= SC= SD. Gọi H là hình chiếu của S lên mặt đáy ABCD . Khẳng định nào sau đây sai?
A. HA = HB = HC = HD
B. Tứ giác ABCD là hình bình hành.
C. Tứ giác ABCD nội tiếp được trong đường tròn.
D. Các cạnh SA, SB, SC, SD hợp với đáy ABCD những góc bằng nhau.
Lời giải:
Chọn B.
Vì hình chóp S.ABCD có các cạnh bên bằng nhau SA = SB = SC = SD và H là hình chiếu của S lên mặt đáy ABCD
⇒ H tâm đường tròn ngoại tiếp tứ giác ABCD
Suy ra HA = HB = HC = HD.
Nên đáp án B sai.
Câu 9: Cho hình chóp S. ABC có các mặt bên tạo với đáy một góc bằng nhau. Hình chiếu H của S trên (ABC) là:
A. Tâm đường tròn nội tiếp tam giác ABC
B. Tâm đường tròn ngoại tiếp tam giác ABC
C. Trọng tâm tam giác ABC
D. Giao điểm hai đường thẳng AC và BD
Lời giải:
Gọi M, N, P lần lượt là hình chiếu của S lên các cạnh AB, AC, BC.
Theo định lý ba đường vuông góc ta có M, N, P lần lượt là hình chiếu của H lên các cạnh AB, AC, BC
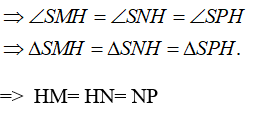
⇒ H là tâm dường tròn nội tiếp của tam giác ABC
Chọn B

