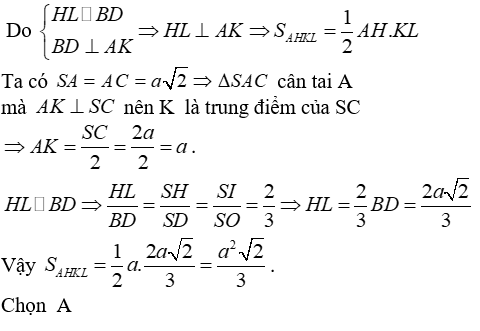Cách tìm thiết diện trong hình học không gian cực hay - Toán lớp 11
Cách tìm thiết diện trong hình học không gian cực hay
Với Cách tìm thiết diện trong hình học không gian cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm thiết diện trong hình học không gian từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải
Để xác định thiết diện của mặt phẳng (α) đi qua điểm O và vuông góc với đường thẳng d với một hình chóp ta thực hiện theo một trong hai cách sau:
Cách 1. Tìm tất cả các đường thẳng vuông góc với d, khi đó (α) sẽ song song hoặc chứa các đường thẳng này và ta chuyển về dạng thiết diện song song như đã biết ở chương II.
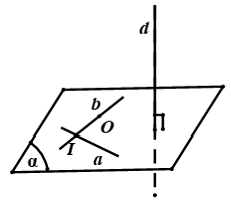
Cách 2. Ta dựng mặt phẳng (α) như sau:
Dựng hai đường thẳng a; b cắt nhau cùng vuông góc với d trong đó có một đường thẳng đi qua O, khi đó (α) chính là mặt phẳng (a; b)
B. Ví dụ minh họa
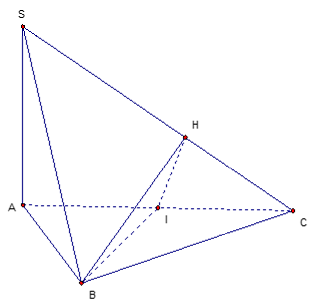
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABC là tam giác đều, SA ⊥ (ABC). Gọi (P) là mặt phẳng qua B và vuông góc với SC. Thiết diện của (P) và hình chóp S.ABC là:
A. Hình thang vuông.
B. Tam giác đều.
C. Tam giác cân.
D. Tam giác vuông.
Hướng dẫn giải
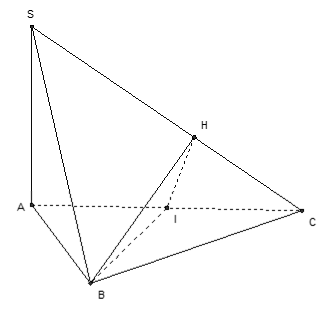
Gọi I là trung điểm của CA, kẻ IH ⊥ SC.
Ta có BI ⊥ AC, BI ⊥ SA ⇒ BI ⊥ SC
Do đó SC ⊥ (BIH) hay thiết diện là tam giác BIH.
Mà BI ⊥ (SAC) nên BI ⊥ IH hay thiết diện là tam giác vuông.
Chọn D
Ví dụ 2: Cho tứ diện đều ABCD cạnh a = 12, gọi (P) là mặt phẳng qua B và vuông góc với AD. Thiết diện của (P) và hình chóp có diện tích bằng
A. 36√2 B. 40 C. 36√3 D. 36
Hướng dẫn giải
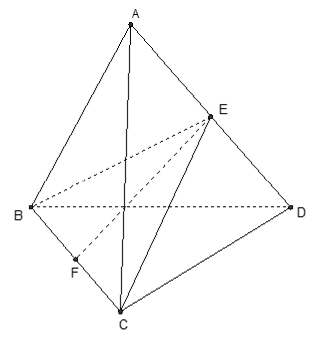
Gọi E là trung điểm AD
Do tam giác ABD đều nên BE ⊥ AD (1)
Do tam giác ACD đều nên CE ⊥ AD (2)
Từ (1) và (2) suy ra: AD ⊥ (BEC)
⇒ Thiết diện là tam giác BCE. Gọi F là trung điểm của BC.
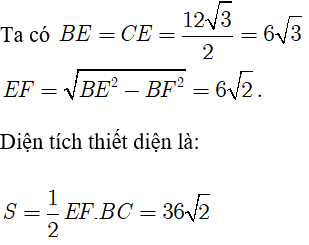
Chọn A
Ví dụ 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , cạnh bên SA ⊥ (ABC) Mặt phẳng (P) đi qua trung điểm M của AB và vuông góc với SB cắt AC, SC, SB lần lượt tại N, P, Q . Tứ giác MNPQ là hình gì ?
A. Hình thang vuông
B. Hình thang cân
C. Hình bình hành
D. Hình chữ nhật
Hướng dẫn giải
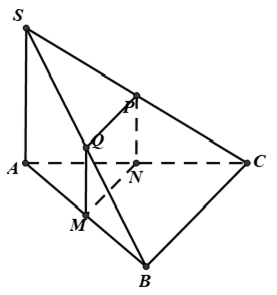
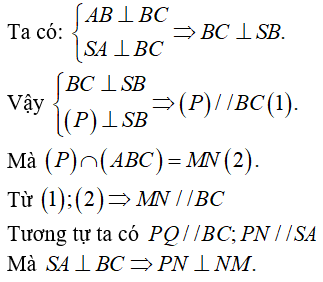
Vậy thiết diện là hình thang MNPQ vuông tại N
Chọn A
Ví dụ 4: Cho hình chóp S.ABC có đáy ABC là tam giác đều, O là trung điểm của đường cao AH của tam giác ABC. SO vuông góc với đáy. Gọi I là điểm tùy ý trên OH (không trùng với O và H). mặt phẳng (P) qua I và vuông góc với OH. Thiết diện của (P) và hình chóp S.ABC là hình gì?
A. Hình thang cân
B. Hình thang vuông
C. Hình bình hành
D. Tam giác vuông
Hướng dẫn giải
+ Mặt phẳng (P) vuông góc với OH nên (P) // SO
Suy ra (P) cắt (SAH) theo giao tuyến là đường thẳng
Qua I và song song với SO cắt SH tại K.
+ Từ giả thiết suy ra (P) // BC, do đó (P) sẽ cắt (ABC) và (SBC) lần lượt là các đường thẳng qua I và K song song với BC cắt AB, AC, SB, SC lần lượt tại M, N, P, Q
Do đó thiết diện là tứ giác MNPQ.
+ Ta có MN và PQ cùng song song BC suy ra I là trung điểm của MN và K là trung điểm của PQ.
Lại có các tam giác ABC đều và tam giác SBC cân tại S suy ra IK vuông góc với MN và PQ dó đó MNPQ là hình thang cân.
Chọn đáp án A.
Ví dụ 5: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b (a > b√2). Gọi G là trọng tâm . Xét mặt phẳng (P) đi qua A và vuông góc với SC tại điểm C1 nằm giữa S và C. Diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (P) là
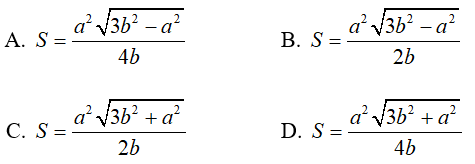
Hướng dẫn giải
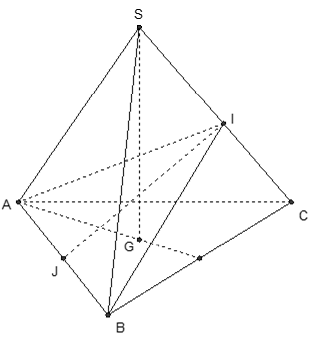
Kẻ AI ⊥ SC ta có: ΔSAC = ΔSBC (c.c.c) nên hai đường cao tương ứng bằng nhau.
⇒ BI ⊥ SC
⇒ (AIB) ⊥ SC. Thiết diện là tam giác AIB.
Ta có
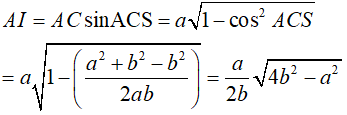
Gọi J là trung điểm của AB. Dễ thấy tam giác AIB cân tại I, suy ra IJ ⊥ AB .
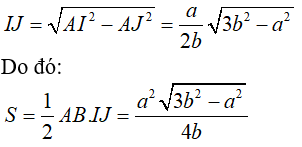
Chọn A
Ví dụ 6: Tam giác ABC có BC = 2a, đường cao AD = a√2. Trên đường thẳng vuông góc với (ABC) tại A, lấy điểm S sao cho SA = a√2. Gọi E; F lần lượt là trung điểm của SB và SC . Diện tích tam giác AEF bằng?
Hướng dẫn giải
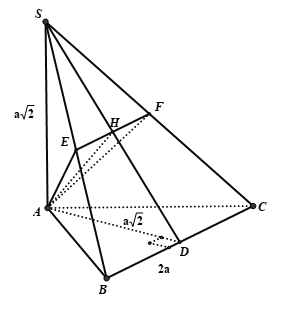

Ví dụ 7: Cho hình chóp S. ABC có đáy ABC là tam giác đều, SA ⊥ (ABC). Gọi (P) là mặt phẳng qua B và vuông góc với SC. Thiết diện của (P) và hình chóp S.ABC là:
A. Hình thang vuông
B. Tam giác đều
C. Tam giác cân
D. Tam giác vuông
Hướng dẫn giải
+ Gọi I là trung điểm của AC, kẻ IH ⊥ SC
Ta có BI ⊥ AC, BI ⊥ SA ⇒ BI ⊥ (SAC)
⇒ BI ⊥ SC. Mà IH ⊥ SC
Do đó SC ⊥ (BIH) hay thiết diện là tam giác BIH .
+ Mà BI ⊥ (SAC) nên BI ⊥ IH hay thiết diện là tam giác vuông.
Chọn D.

C. Bài tập vận dụng
Câu 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, SA ⊥ (ABC), SA = a(√3/2). Gọi (P) là mặt phẳng đi qua A và vuông góc với BC. Thiết diện của hình chóp S.ABC được cắt bởi (P) có diện tích bằng?

Lời giải:
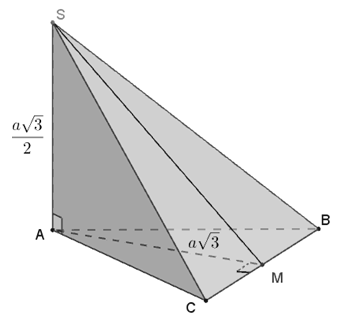
Gọi M là trung điểm của BC thì BC ⊥ AM (1)
Hiển nhiên AM = a√3.
Mà SA ⊥ (ABC) ⇒ BC ⊥ SA (2)
Từ (1) và ( 2) suy ra BC ⊥ (SAM) ⇒ (P) ≡ (SAM)
Khi đó thiết diện của hình chóp S.ABC được cắt bởi (P) chính là tam giác SAM
Do tam giác SAM vuông tại A nên
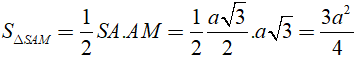
Chọn đáp án C
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC), SA = a. Gọi (P) là mặt phẳng đi qua S và vuông góc với BC. Thiết diện của (P) và hình chóp S.ABC có diện tích bằng ?
Lời giải:
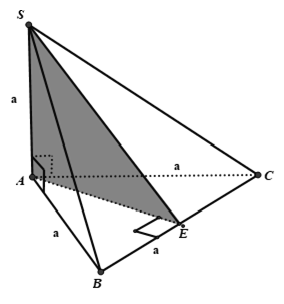
Kẻ AE ⊥ BC, SA ⊥ BC ⇒ BC ⊥ (SAE) ≡ (P)
Thiết diện của mặt phẳng (P) và hình chóp S.ABC là tam giác SAE.
Tam giác SAE vuông tại A vì SA ⊥ (ABC), có:
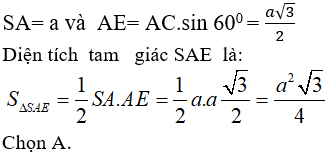
Câu 3: Cho tứ diện SABC có hai mặt (ABC) và (SBC) là hai tam giác đều cạnh a, SA = a(√3/2). M là điểm trên AB sao cho AM = b ( 0 < b < a) . (P) là mặt phẳng qua M và vuông góc với BC. Thiết diện của (P) và tứ diện SABC có diện tích bằng?
Lời giải:
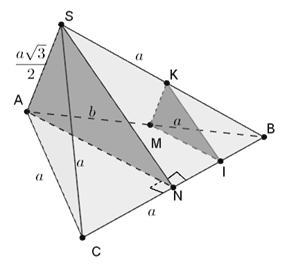
Gọi N là trung điểm của BC.
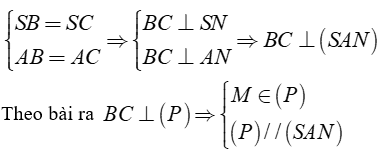
Kẻ MI // AN, MK // SA ⇒ Thiết diện của (P) và tứ diện SABC là tam giác KMI.

Câu 4: Cho tứ diện đều ABCD cạnh a = 12; AP là đường cao của tam giác ACD. Mặt phẳng (P) qua B vuông góc với AP cắt mp (ACD) theo đoạn giao tuyến có độ dài bằng ?
A. 9 B. 6 C. 8 D. 7
Lời giải:
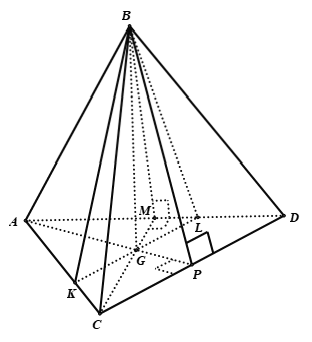
Ta có: CD ⊥ AP, CD ⊥ BP ⇒ CD ⊥ (APB) ⇒ BG ⊥ CD
Tương tự: AD ⊥ CM, AD ⊥ BM ⇒ AD ⊥ (BCM) ⇒ AD ⊥ BG
Suy ra: BG ⊥ (ABC) ⇒ BG ⊥ AP
Kẻ KL đi qua trọng tâm G của tam giác ACD và song song với CD
⇒ AP ⊥ KL ⇒ (P) chính là mặt phẳng (BKL)
(ACD) ∩ (BKL) = KL = (2/3)CD = 8
Có thể nói nhanh theo tính chất tứ diện đều:
Gọi G là trọng tâm ΔACD thì G là tâm đường tròn ngoại tiếp tam giác ACD nên BG ⊥ (ACD)
Trong mp(ACD) kẻ qua G đường thẳng song song với CD cắt AC, AD lần lượt tại K, L
(BKL) ⊥ (ACD), AP ⊥ KL ⇒ AP ⊥ (BKL).
(P) ≡ (BKL)
(ACD) ∩ (BKL) = KL = (2/3) CD = 8
Chọn C
Câu 5: Cho hình chóp S.ABCD, với đáy ABCD là hình thang vuông tại A, đáy lớn AD = 8 ; BC = 6, SA vuông góc với mặt phẳng (ABCD), SA = 6. Gọi M là trung điểm AB. (P) là mặt phẳng qua M và vuông góc với AB. Thiết diện của (P) và hình chóp có diện tích bằng?
A. 10 B. 20 C. 15 D. 16
Lời giải:
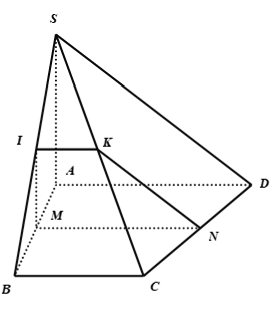
Do (P) ⊥ AB ⇒ (P) // SA
Gọi I là trung điểm của SB ⇒ MI // SA ⇒ MI ⊂ (P)
Gọi N là trung điểm của CD ⇒ MN ⊥ AB ⇒ MN ⊂ (P)
Gọi K là trung điểm của SC ⇒ IK // BC,
mà MN // BC nên MN // IK
Vậy thiết diện của (P) và hình chóp là hình thang MNKI vuông tại M
Ta có:
MI là đường trung bình của tam giác SAB ⇒ MI = (1/2)SA = 3
IK là đường trung bình của tam giác SBC ⇒ IK = (1/2)BC = 3
MN là đường trung bình của hình thang ABCD ⇒ MN = (1/2)(AD + BC) = 7
Khi đó 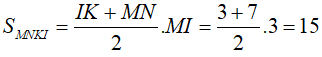
Chọn đáp án C
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a. Gọi I; K lần lượt là trung điểm các cạnh AB và SC . Tính IK.
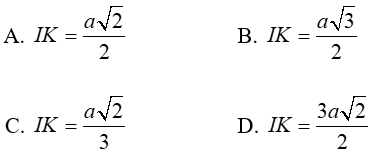
Lời giải:
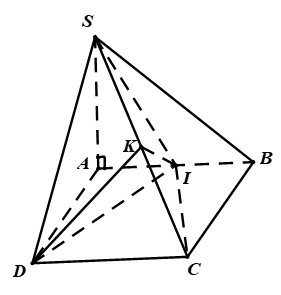

Câu 7: Cho hình vuông ABCD có tâm O và cạnh bằng 2a. Trên đường thẳng qua O vuông góc với (ABCD) lấy điểm S. Biết góc giữa SA và (ABCD) có số đo bằng 45°. Tính độ dài SO.

Lời giải:
Chọn B

Câu 8: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB = a; SA = a√3 và SA ⊥ (ABCD) . Gọi M là điểm trên cạnh AB và AM = x (0 < x < a) , mặt phẳng (α) đi qua M và vuông góc với AB. Giả sử thiết diện của hình chóp S.ABC với (α) là tứ giác MNPQ. Hỏi tứ giác MNPQ là hình gì
A. Hình chữ nhật
B. hình vuông
C. hình thang
D. hình bình hành
Lời giải:
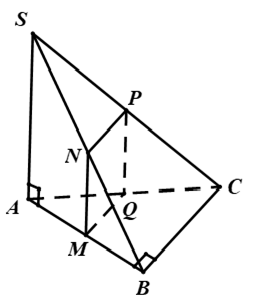
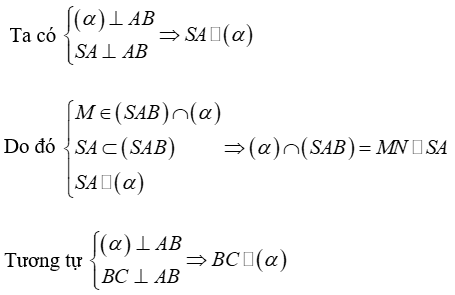

Chọn đáp án A
Câu 9: Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc và AB = a, BC = b, CD = c. Độ dài AD:
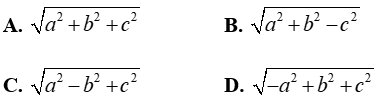
Lời giải:
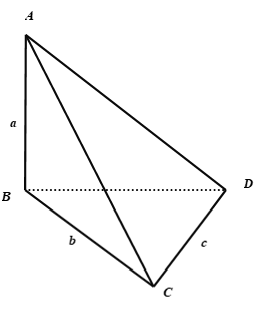
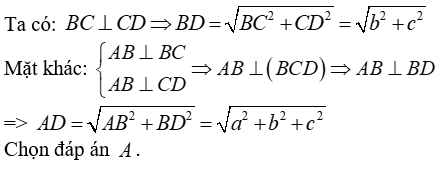
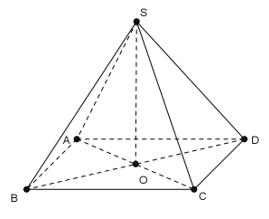
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a√2. Giả sử tồn tại tiết diện của hình chóp với mặt phẳng (α) đi qua A vuông góc với SC. Tính diện tích thiết diện.
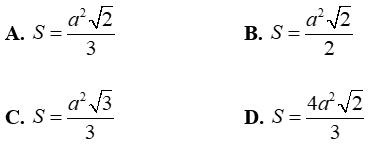
Lời giải:
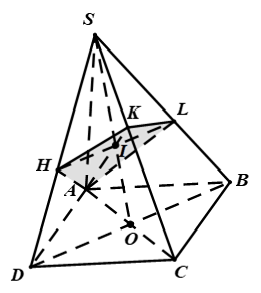
* Ta đi tìm thiết diện của hình chóp cắt bởi mp(α)
Gọi K là hình chiếu của A trên SC thì K ∈ (α) .Trong (SAC) gọi I là giao điểm của SO và AK.
Ta có
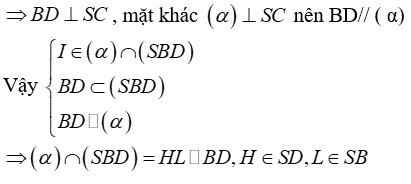
Thiết diện là tứ giác AHKL
* Tính diện tích thiết diện: