Lý thuyết Phép vị tự hay, chi tiết nhất - Toán lớp 11

Lý thuyết Phép vị tự hay, chi tiết nhất

Tài liệu Lý thuyết Phép vị tự hay, chi tiết nhất Toán lớp 11 sẽ tóm tắt kiến thức trọng tâm về Phép vị tự từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 11.

1. Định nghĩa

    Cho điểm O và số k ≠ 0. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho OM'→ = kOM→ được gọi là phép vị tự tâm O tỉ số k.

    Phép vị tự tâm O tỉ số k thường được kí hiệu là V_(O;k).

Nhận xét

    Phép vị tự biến tâm vị tự thành chính nó.

    Khi k = 1, phép vị tự là đồng nhất.

    Khi k = –1, phép vị tự là phép đối xứng tâm.

    M’ = V_{(O; k)}(M) ⇔ M = V_{(O; 1/k)}(M’)

2. Tính chất

Tính chất 1

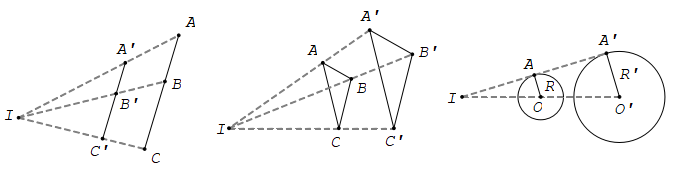
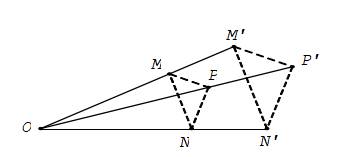
    Nếu phép vị tự tỉ số k biến hai điểm M, N tùy ý theo thứ tự thành M’, N’ thì M'N'→ = kMN→ và M’N’ = |k|.MN.

Tính chất 2

Phép vị tự tỉ số k:

    Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy;

    Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng;

    Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó;

    Biến đường tròn bán kính R thành đường tròn bán kính |k|R.