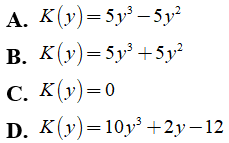Bài tập Cộng, trừ đa thức một biến có lời giải - Toán lớp 7

---

Bài tập Cộng, trừ đa thức một biến có lời giải

Với bộ Bài tập Cộng, trừ đa thức một biến Toán lớp 7 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 7.

Bài 1: Tìm hai đa thức P(x) và Q(x) sao cho P(x) + Q(x) = x² + 1

A. P(x) = x²; Q(x) = x + 1

B. P(x) = x² + x; Q(x) = x + 1

C. P(x) = x²; Q(x) = -x + 1

D. P(x) = x² - x; Q(x) = x + 1

Hiển thị lời giải

Ta có với P(x) = x² - x; Q(x) = x + 1

P(x) + Q(x) = x² - x + x + 1 = x² + 1

Chọn đáp án D

Bài 2: Cho f(x) = x⁵ - 3x⁴ + x² - 5 và g(x) = 2x⁴ + 7x³ - x² + 6. Tìm hiệu f(x) - g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:

A. 11 + 2x² + 7x³ - 5x⁴ + x⁵

B. -11 + 2x² - 7x³ - 5x⁴ + x⁵

C. x⁵ - 5x⁴ - 7x³ + 2x² - 11

D. x⁵ - 5x⁴ - 7x³ + 2x² + 11

Hiển thị lời giải

Ta có

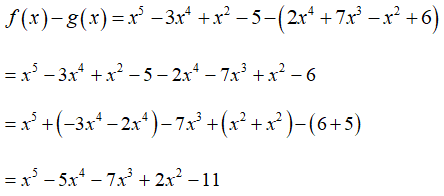
Sắp xếp theo lũy thừa tăng dần của biến ta được

-11 + 2x² - 7x³ - 5x⁴ + x⁵

Chọn đáp án B

Bài 3: Cho p(x) = 5x⁴ + 4x³ - 3x² + 2x - 1 và q(x) = -x⁴ + 2x³ - 3x² + 4x - 5

Tính p(x) + q(x) rồi tìm bậc của đa thức thu được

A. p(x) + q(x) = 6x³ - 6x² + 6x - 6 có bậc là 6

B p(x) + q(x) = 4x⁴ + 6x³ - 6x² + 6x + 6 có bậc là 4

C. p(x) + q(x) = 4x⁴ + 6x³ - 6x² + 6x - 6 có bậc là 4

D. P(x) + q(x) = 4x⁴ + 6x³ + 6x - 6 có bậc là 4

Hiển thị lời giải

Ta có p(x) + q(x)

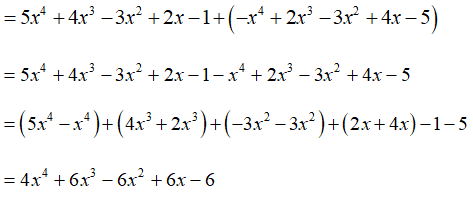
Bậc của đa thức p(x) + q(x) = 4x⁴ + 6x³ - 6x² + 6x - 6 là 4

Chọn đáp án C

Bài 4: Tìm đa thức h(x) biết f(x) - h(x) = g(x) biết

f(x) = x² + x + 1; g(x) = 4 - 2x³ + x⁴ + 7x⁵

A. h(x) = -7x⁵ - x⁴ + 2x³ + x² + x - 3

B. h(x) = 7x⁵ - x⁴ + 2x³ + x² + x + 3

C. h(x) = -7x⁵ - x⁴ + 2x³ + x² + x + 3

D. h(x) = 7x⁵ + x⁴ + 2x³ + x² + x + 3

Hiển thị lời giải

Ta có f(x) - h(x) = g(x) ⇒ h(x) = f(x) - g(x)

Mà f(x) = x² + x + 1; g(x) = 4 - 2x³ + x⁴ + 7x⁵ nên h(x) = x² + x + 1 - (4 - 2x³ + x⁴ + 7x⁵)

= x² + x + 1 - 4 + 2x³ - x⁴ - 7x⁵

= -7x⁵ - x⁴ + 2x³ + x² + x - 3

Vậy h(x) = -7x⁵ - x⁴ + 2x³ + x² + x - 3

Chọn đáp án A

Bài 5: Tìm hệ số cao nhất của đa thức k(x) biết f(x) + k(x) = g(x) và f(x) = x⁴ - 4x² + 6x³ + 2x - 1; g(x) = x + 3

A. -1            B. 1            C. 4            D. 6

Hiển thị lời giải

Ta có f(x) + k(x) = g(x) ⇒ k(x) = g(x) - f(x)

= x + 3 - (x⁴ - 4x² + 6x³ + 2x - 1)

= x + 3 - x⁴ + 4x² - 6x³ - 2x + 1 = -x⁴ - 6x³ + 4x² - x + 4

Nhận thấy số hạng có lũy thừa cao nhất của biến là -x⁴ nên hệ số cao nhất là -1

Chọn đáp án A

Bài 6: Tìm hệ số tự do của hiệu f(x) - 2.g(x) với

f(x) = 5x⁴ + 4x³ - 3x² + 2x - 1; g(x) = -x⁴ + 2x³ - 3x² + 4x + 5

A. 7            B. 11            C. -11            D. 4

Hiển thị lời giải

- Ta có:

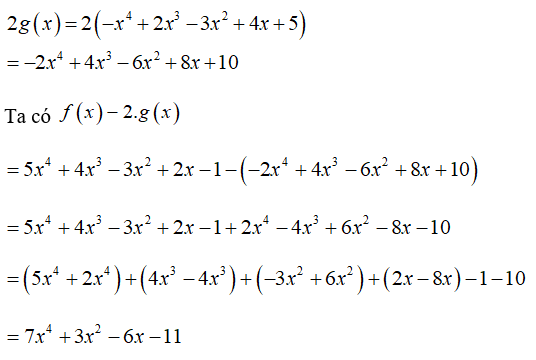
Hệ số cần tìm là -11

Chọn đáp án C

Bài 7: Cho biết M(x) + (x³ + 5x² - 7x + 1) = 3x⁴ + x³ - 7 . Câu nào sau đây đúng:

A. M(x) = 3x⁴ + x³ - 7

B. Bậc của M(x) là 4

C. Hệ số cao nhất của M(x) là 7

D. A, B đúng và C sai

Hiển thị lời giải

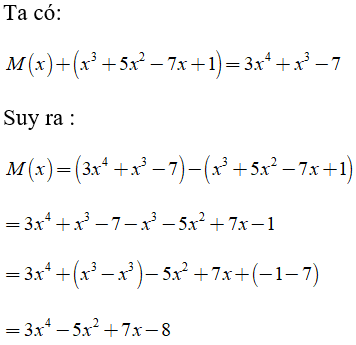
Bậc của đa thức M(x) là 4

Hệ số cao nhất của M(x) là 3

Suy ra đáp án A, C, D sai, B đúng

Chọn đáp án B

Bài 8: Cho hai đa thức A(x) = 4x² + 5x + 3 và B(x) = - 4x² + 5x⁷ - 5x + 3 . Tìm bậc của đa thức C(x) với C(x) = A(x) + B(x)

A. 2

B. 3

C. 5

D. 7

Hiển thị lời giải

Ta có:

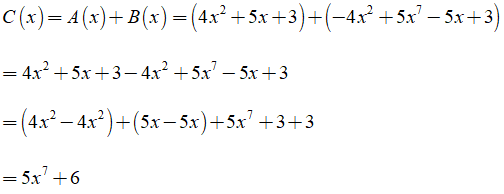
Vậy bậc của đa thức C(x) là 7.

Chọn đáp án D

Bài 9: Cho hai đa thức M(y) = 5y³ + y - 6 và N(y) = 5y² + y - 6 . Tìm đa thức K(y) = M(y) - N(y)

Hiển thị lời giải

Ta có:

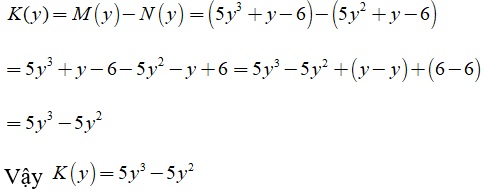
Chọn đáp án A

Bài 10: Thu gọn đa thức (5x³ + 4x² - 1) - (4x³ - 4x² + 1) ta được

A. 0

B. x³ + 8x² - 2

C. -x³ + 8x² - 2

D. -x³ - 8x² - 2

Hiển thị lời giải

Ta có:

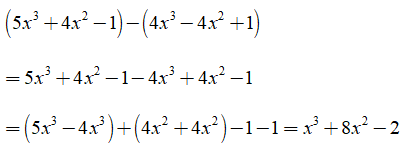
Chọn đáp án B