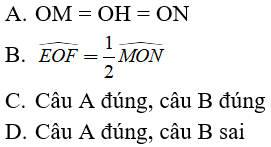Bài tập Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c) có lời giải - Toán lớp 7
Bài tập Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c) có lời giải
Với bộ Bài tập Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c) Toán lớp 7 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 7.

Bài 1: Cho tam giác ABC và tam giác MNK có: AB = MN, ∠A = ∠M. Cần điều kiện gì để tam giác ABC bằng với tam giác MNK?
A. BC = MK B. BC = HK C. AC = MK D. AC = HK
Để tam giác ABC bằng tam giác MNK theo trường hợp cạnh – góc – cạnh thì ta cần thêm điều kiện là AC = MK
Chọn đáp án C.
Bài 2: Cho tam giác BAC và tam giác KEF có BA = EK, ∠A = ∠K, CA = KF. Phát biểu nào sau đây đúng?
A. ΔBAC = ΔEKF
B. ΔBAC = ΔEFK
C. ΔABC = ΔFKE
D. ΔBAC = ΔKEF
Xét hai tam giác BAC và tam giác KEF có: BA = EK, ∠A = ∠K, CA = KF
Suy ra ΔBAC = ΔEKF (c-g-c)
Chọn đáp án A.
Bài 3: Cho hai đoạn thẳng BD và EC vuông góc với nhau tại A sao cho AB = AE, AD = AC, AB < AC. Phát biểu nào sau đây sai?
A. ΔAED = ΔABC
B. BC = ED
C. EB = CD
D. ∠ABC = ∠AED
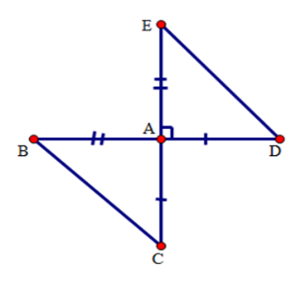
Xét hai tam giác ABC và AED có: AB = AE; ∠BAC = ∠DAE; AD = AC
Suy ra: ΔAED = ΔABC (c-g-c) nên A đúng
Suy ra BC = ED (cạnh tương ứng) nên B đúng; ∠ABC = ∠AED (hai góc tương ứng) nên D đúng
Vậy đáp án C sai.
Chọn đáp án C.
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB; OC = OD (A nằm giữa O và C; B nằm giữa O và D)
(Áp dụng câu 4 – câu 5)
Bài 4: Chọn câu đúng
A. ΔOAD = ΔOCB
B. ΔODA = ΔOBC
C. ΔAOD = ΔBCO
D. ΔOAD = ΔOBC
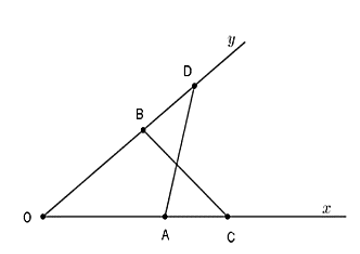
Xét tam giác OAD và tam giác OBC có:
OA = OB; góc O chung; OC = OD
Suy ra: ΔOAD = ΔOBC (c-g-c)
Chọn đáp án D.
Bài 5: So sánh hai góc ∠CAD và ∠CBD
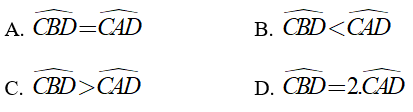

Bài 6: Cho góc nhọn xOy. Lấy điểm H nằm trong góc xOy. Từ H kẻ HE ⊥ Ox tại E, HF ⊥ Oy tại F. Trên tia HE lấy điểm sao cho E là trung điểm của HM, trên tia HF lấy điểm N sao cho F là trung điểm của HN. Khi đó:
Chọn đáp án C
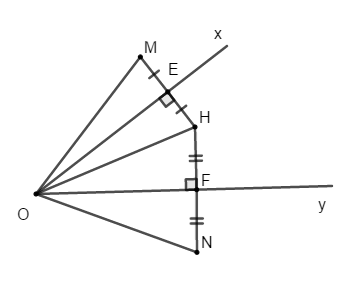
Bài 7: Cho tam giác ABC có B^ = C^. Trên tia đối của tia BA lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho BM = CN. So sánh CM và BN.
A. BN = CM
B. BN < CM
C. BN > CM
D. BN = 2CM
Chọn đáp án A
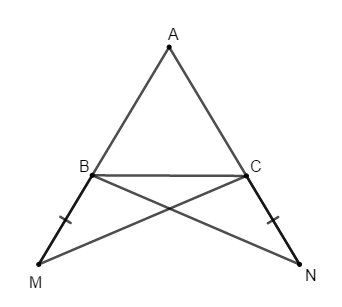
Bài 8: Cho tam giác ABC. Qua A kẻ đường thẳng d // BC, trên d lấy điểm E sao cho AE = BC (E nằm khác phía với B so với AC). Chọn câu sai
A. ΔABC = ΔCEA
B. AB = EC
C. 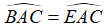
D. AB // EC
Chọn đáp án C
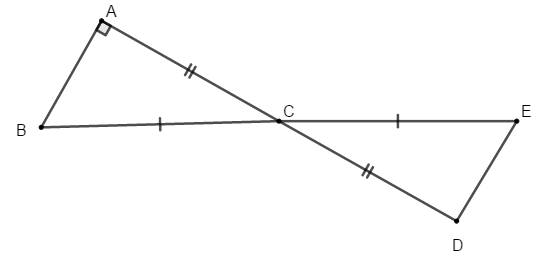
Bài 9: Cho tam giác ABC vuông tại A. Trên tia đối của tia CA, lấy điểm D sao cho cho CA = CD. Trên tia đối của tia CB, lấy điểm E sao cho CB = CE. Số đo góc 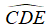
A. 80°
B. 90°
C. 100°
D. 110°
Chọn đáp án B
Bài 10: Cho tam giác DEF và tam giác MNP có DE = MN, E^ = N^, EF = NP. Biết D^ = 80°, số đo góc M^ là:
A. 60°
B. 70°
C. 80°
D. 90°
Chọn đáp án C