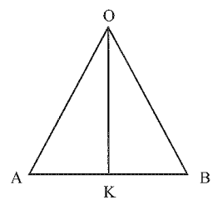
Cho tam giác OAB cân tại O, OK là đường phân giác của góc O

Cho tam giác OAB cân tại O, OK là đường phân giác của góc O. Chứng minh OK là đường trung trực của AB.

Giải vở thực hành Toán 7 Bài 5: Đường trung trực của một đoạn thẳng

Bài 3 trang 49 Vở thực hành Toán 7 Tập 2: Cho tam giác OAB cân tại O, OK là đường phân giác của góc O. Chứng minh OK là đường trung trực của AB.

Lời giải:

Xét tam giác KOA và tam giác KOB.

OA = OB ( do tam giác OAB cân tại O)

Góc AOK = góc BOK ( do OK là đường phân giác của góc O)

Cạnh chung OK.

Vậy tam giác KOA = tam giác KOB theo trường hợp c.g.c.

Suy ra KA = KB (1) và $\widehat{\text{OKB}}=\widehat{\text{OKA}}\text{}$

Do $\widehat{\text{OKB}}+\widehat{\text{OKA}}=180°$ nên $\widehat{\text{OKB}}=90°$ suy ra OK vuông góc với AB (2).

Từ (1) và (2) suy ra OK là đường trung trực của AB.