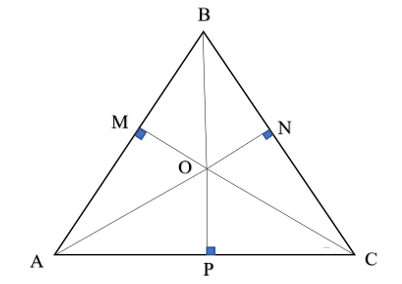
Cho tam giác ABC, O là điểm bên trong tam giác. Từ O hạ đường vuông góc OM, ON, OP

Cho tam giác ABC, O là điểm bên trong tam giác. Từ O hạ đường vuông góc OM, ON, OP lần lượt tới các cạnh AB, BC, CA và có OM = ON = OP. Chứng minh O là giao điểm của ba đường phân giác của tam giác ABC.

Giải vở thực hành Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác

Bài 5 trang 62 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC, O là điểm bên trong tam giác. Từ O hạ đường vuông góc OM, ON, OP lần lượt tới các cạnh AB, BC, CA và có OM = ON = OP. Chứng minh O là giao điểm của ba đường phân giác của tam giác ABC.

Lời giải:

Xét hai tam giác OMA và OPA:

OM = OP ( gt).

$\widehat{\text{OMA}}=\widehat{\text{OPA}}=90°$.

Cạnh chung OA.

Vậy tam giác OMA bằng tam giác OPA theo trường hợp c.g.c. Suy ra $\widehat{\text{OAM}}=\widehat{\text{OAP}}$hay AO là tia phân giác của góc A. (1)

Tương tự xét hai tam giác OCP và OCN:

OP = ON (gt).

$\widehat{\text{OPC}}=\widehat{\text{ONC}}\text{}$.

Cạnh chung OC.

Vậy tam giác OCP bằng tam giác OCN theo trường hợp c.g.c. Suy ra $\widehat{\text{OCP}}=\widehat{\text{OCN}}$ hay CO là tia phân giác của góc A. (1)

Từ (1) và (2) suy ra O là giao điểm của 3 đường phân giác của tam giác ABC.