Giải Vở thực hành Toán 7 trang 54 Tập 2 Chân trời sáng tạo

---

Với Giải VTH Toán 7 trang 54 Tập 2 trong Bài 7: Tính chất ba đường trung tuyến của tam giác Vở thực hành Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 54.

Giải VTH Toán 7 trang 54 Tập 2 Chân trời sáng tạo

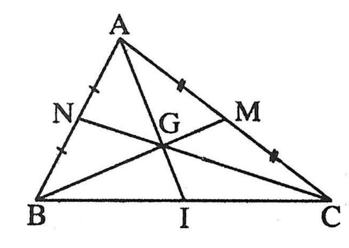
Câu 2 trang 54 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC, AM là đường trung tuyến, G là trọng tâm. Ta có:

A. $\frac{\text{AG}}{\text{AM}}=\frac{2}{3}$;

B. $\frac{\text{GA}}{\text{AM}}=\frac{1}{2}$;

C. $\frac{\text{GM}}{\text{GA}}=\frac{1}{3}$;

D. $\frac{\text{GA}}{\text{GM}}=\frac{2}{3}$;

Lời giải:

Theo định lí về đường trung tuyến của tam giác, khi AM là trung tuyến, G là trọng tâm, ta có: $\frac{\text{AG}}{\text{AM}}=\frac{2}{3}$.

Vậy chọn đáp án A.

Bài 1 trang 54 Vở thực hành Toán 7 Tập 2: Vẽ ba hình: tam giác nhọn, tam giác tù, tam giác vuông; rồi vẽ ba đường trung tuyến của mỗi tam giác đó.

Lời giải:

Tam giác nhọn ABC có ba đường trung tuyến là AI, BM, CN.

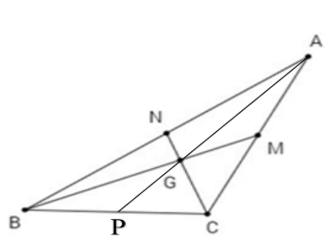
Tam giác tù ABC có các đường trung tuyến AP, CN, BM.

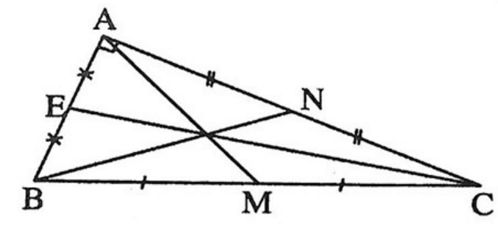
Tam giác ABC vuông tại A có các đường trung tuyến AM, BN, CE.

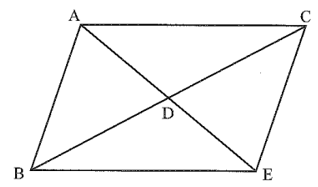
Bài 2 trang 54 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC có AD là trung tuyến. Trên tia đối của tia DA lấy điểm E, sao cho DA = DE. Chứng minh:

a) AB song song và bằng CE.

b) AC song song và bằng BE.

Lời giải:

a) AD là trung tuyến của tam giác ABC nên DB = DC.

Xét tam giác ADB và tam giác EDC

DB = DC.

DA = DE (gt).

$\widehat{\text{ADB}}$= $\widehat{\text{EDC}}$( hai góc đối đỉnh).

Vậy tam giác ADB bằng tam giác EDC. Suy ra $\widehat{ABD}=\widehat{ECD}$mà hai góc ở vị trí so le trong nên AB // CE.

b) Xét tam giác ADC và tam giác EDB

DC = DB.

DA = DE (gt).

$\widehat{\text{ADC}}$= $\widehat{\text{EDB}}$( hai góc đối đỉnh).

Vậy tam giác ADC bằng tam giác EDB theo trường hợp c.g.c. Suy ra

$\widehat{\text{ADC}}$= $\widehat{\text{EDB}}$ mà đây là hai góc so le trong nên AC // BE.

Lời giải Vở thực hành Toán 7 Bài 7: Tính chất ba đường trung tuyến của tam giác Chân trời sáng tạo hay khác:

• Giải VTH Toán 7 trang 53 Tập 2

• Giải VTH Toán 7 trang 55 Tập 2

• Giải VTH Toán 7 trang 56 Tập 2