Giải Vở thực hành Toán 7 trang 56 Tập 2 Chân trời sáng tạo

---

Với Giải VTH Toán 7 trang 56 Tập 2 trong Bài 7: Tính chất ba đường trung tuyến của tam giác Vở thực hành Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 56.

Giải VTH Toán 7 trang 56 Tập 2 Chân trời sáng tạo

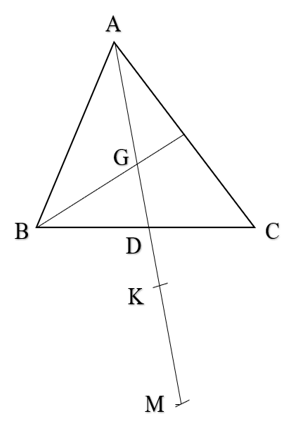
Bài 7 trang 56 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC có trung tuyến AD và G là trọng tâm của tam giác trên tia đối của DA lấy hai điểm K và M, sao cho DK = DG và DA = DM. Chứng minh AG = GK = KM.

Lời giải:

Theo định lí ba đường trung tuyến của tam giác ta có: AG = $\frac{2}{3}$AD. Suy ra GD = $\frac{1}{2}$AG hay 2DG = AG.

Có DK = DG (gt) nên: GK = DK + DG = 2DG = AG. (1)

Có DA = DM (gt) nên: GA + GD = DK + KM mà GD = DK nên GA = KM. (2)

Vậy từ (1) và (2) suy ra AG = GK = KM.

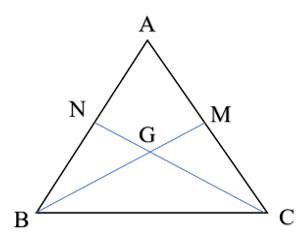
Bài 8 trang 56 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC có hai trung tuyến BM và CN cắt nhau tại G. Biết BM = CN, chứng minh tam giác GBC và tam giác GMN cùng cân tại G.

Lời giải:

Theo định lí về ba đường trung tuyến trong tam giác ta có:

GC = $\frac{2}{3}$CN.

GB = $\frac{2}{3}$BM.

Mà BM = CN (gt) nên GB = GC. Suy ra tam giác GBC cân tại G.

GN = CN – GC = BM – GB = GM. Suy ra tam giác GMN cân tại G.

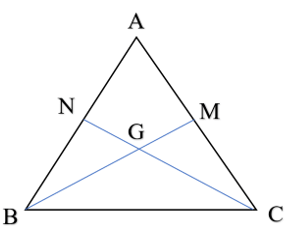
Bài 9 trang 56 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC có hai trung tuyến BM và CN cắt nhau tại G. Biết BM = CN. Chứng minh tam giác ABC cân tại A.

Lời giải:

Theo định lí về ba đường trung tuyến trong tam giác ta có:

GC = $\frac{2}{3}$CN.

GB = $\frac{2}{3}$BM.

Mà BM = CN (gt) nên GB = GC. Suy ra tam giác GBC cân tại G, nên $\widehat{\text{NCB}}=\widehat{\text{MBC}}\text{}$.

Xét tam giác NCB và tam giác MBC:

BM = CN (gt).

$\widehat{\text{NCB}}=\widehat{\text{MBC}}\text{}$.

Cạnh chung BC.

Nên tam giác NCB bằng tam giác MBC theo trường hợp c.g.c.

Ta được $\widehat{\text{NBC}}=\widehat{\text{MCB}}$(hai góc tương ứng) hay $\widehat{\text{ABC}}=\widehat{\text{ACB}}$suy ra tam giác ABC cân tại A.

Lời giải Vở thực hành Toán 7 Bài 7: Tính chất ba đường trung tuyến của tam giác Chân trời sáng tạo hay khác:

• Giải VTH Toán 7 trang 53 Tập 2

• Giải VTH Toán 7 trang 54 Tập 2

• Giải VTH Toán 7 trang 55 Tập 2