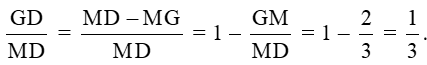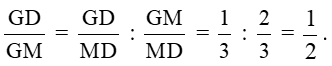Giải Vở thực hành Toán 7 trang 55 Tập 2 Chân trời sáng tạo

---

Với Giải VTH Toán 7 trang 55 Tập 2 trong Bài 7: Tính chất ba đường trung tuyến của tam giác Vở thực hành Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 55.

Giải VTH Toán 7 trang 55 Tập 2 Chân trời sáng tạo

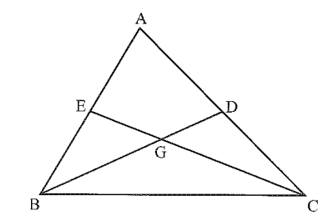
Bài 3 trang 55 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC có BD và CE là hai trung tuyến. G là trọng tâm. Hãy điền số thích hợp vào chỗ chấm:

BG = ....... GD; GD = .......... BG; EC = ........ GE.

Lời giải:

Theo định lí về ba đường trung tuyến của tam giác, ta điền được như sau:

BG = 2 GD; GD = $\frac{1}{2}$BG; EC = 3 GE.

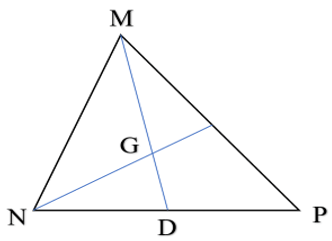
Bài 4 trang 55 Vở thực hành Toán 7 Tập 2: Cho tam giác MNP có MD là trung tuyến, G là trọng tâm của tam giác. Hãy tính các tỉ số: $\frac{\text{GD}}{\text{GM}};\frac{\text{GD}}{\text{MD}};\frac{\text{GM}}{\text{MD}}$.

Lời giải:

Theo định lí về ba đường trung tuyến của tam giác, ta có $\frac{\text{GM}}{\text{MD}}$= $\frac{2}{3}$.

Suy ra

Do đó

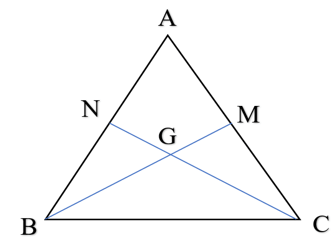
Bài 5 trang 55 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC cân tại A, hai trung tuyến BM và CN cắt nhau tại G.

a) Chứng minh BM = CN.

b) Biết BM = 9 cm. Tính CG.

Lời giải:

a) Tam giác ABC cân tại A nên AB = AC và $\widehat{\text{ABC}}=\widehat{\text{ACB}}$.

BM là trung tuyến nên M là trung điểm AC. Ta có MA = MC = $\frac{1}{2}$AC.

CN là trung tuyến nên N là trung điểm AB. Ta có NA = NB = $\frac{1}{2}$AB.

Suy ra MA = MC = NA = NB.

Xét tam giác CNB và tam giác BMC.

NB = MC.

$\widehat{\text{NBC}}=\widehat{\text{MCB}}$.

Cạnh chung BC.

Vậy tam giác CNB bằng tam giác BMC theo trường hợp c.g.c. Suy ra BM = CN.

b) Do BM = CN nên BM = 9 cm thì CN = 9 cm.

Theo định lí về ba đường trung tuyến của tam giác, CG = <![if !vml]><![endif]>CN.

Suy ra CG = $\frac{2}{3}$.9 = 6 cm.

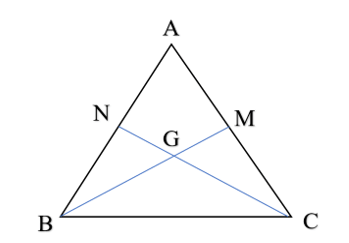
Bài 6 trang 55 Vở thực hành Toán 7 Tập 2: Cho tam giác ABC có hai trung tuyến BM và CN cắt nhau tại G. Biết BM = CN. Chứng minh tam giác GBC và tam giác GMN cân tại G.

Lời giải:

Theo định lí về ba đường trung tuyến trong tam giác ta có:

GC = $\frac{2}{3}$CN.

GB = $\frac{2}{3}$BM.

Mà BM = CN (gt) nên GB = GC. Suy ra tam giác GBC cân tại G.

GN = CN – GC = BM – GB = GM. Suy ra tam giác GMN cân tại G.

Lời giải Vở thực hành Toán 7 Bài 7: Tính chất ba đường trung tuyến của tam giác Chân trời sáng tạo hay khác:

• Giải VTH Toán 7 trang 53 Tập 2

• Giải VTH Toán 7 trang 54 Tập 2

• Giải VTH Toán 7 trang 56 Tập 2