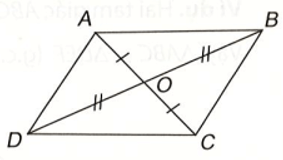
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như hình bên

Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như hình bên.

Giải Vở thực hành Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Bài 2 (4.13) trang 64 vở thực hành Toán lớp 7 Tập 1: Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như hình bên.

a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau.

b) Chứng minh rằng $\Delta DAB=\Delta BC\text{D}.$

Lời giải:

a) Theo hình vẽ bên ta có: ∆AOD = ∆COB (c – g – c), vì:

OA = OC (theo giả thiết), $\widehat{AO\text{D}}=\widehat{COB}$ (2 góc đối đỉnh), OD = OB (theo giả thiết).

∆AOB = ∆COD (c – g – c), vì:

OA = OC (theo giả thiết), $\widehat{AOB}=\widehat{CO\text{D}}$ (2 góc đối đỉnh), OB = OD (theo giả thiết).

b) ∆DAB và ∆BCD có:

$\widehat{ADB}=\widehat{CBD}$ (vì ∆AOD = ∆COB)

BD chung

$\widehat{ABD}=\widehat{CDB}$ (vì ∆AOB = ∆COD)

Do đó ∆DAB = ∆BCD (g – c – g).