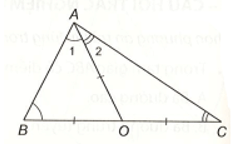
Xét điểm O cách đều ba đỉnh của tam giác ABC

Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.

Giải vở thực hành Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Bài 2 (9.28) trang 82 vở thực hành Toán lớp 7 Tập 2: Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.

Lời giải:

Giả sử O nằm trên cạnh BC thì theo giả thiết, OB = OC nên O là trung điểm của BC.

Từ giả thiết OA = OB = OC nên tam giác OAB cân tại O, tam giác OAC cân tại O.

Vậy $\widehat{A}=\widehat{A_1}+\widehat{A_2}=\widehat{B}+\widehat{C}$, mà $\widehat{A}+\widehat{B}+\widehat{C}=180°$, hay $2\widehat{A}=180°$, suy ra $\widehat{A}=180°$ hay tam giác ABC vuông tại A.