Cho ba điểm phân biệt thẳng hàng A, B, C

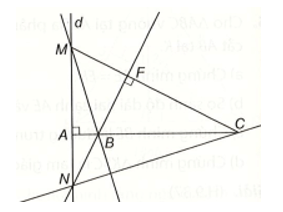
Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với đường thẳng AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.

Giải vở thực hành Toán 7 Luyện tập chung trang 84,85 Tập 2

Bài 2 (9.32) trang 84 vở thực hành Toán lớp 7 Tập 2: Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với đường thẳng AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.

Lời giải:

Gọi giao của BN và CM là F thì NF ⊥ MC tại F.

Trong tam giác MNC có CA $\perp$ MN (vì d ⊥ AB tại A), NF $\perp$ MC, AC giao với NF tại B nên B là trực tâm của tam giác MNC.

Suy ra BM là đường cao của tam giác MNC hay BM vuông góc với đường thẳng CN.