Kí hiệu SABC là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC

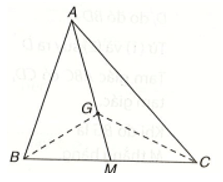
Kí hiệu S là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC.

Giải vở thực hành Toán 7 Luyện tập chung trang 84,85 Tập 2

Bài 4 (9.35) trang 84 vở thực hành Toán lớp 7 Tập 2: Kí hiệu S_ABC là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC.

a) Chứng minh S_GBC = $\frac{1}{3}$S_ABC.

Gợi ý. Sử dụng GM = $\frac{1}{3}$AM để chứng minh S_GBM = $\frac{1}{3}$S_ABM, S_GCM = $\frac{1}{3}$S_ACM.

b) Chứng minh S_GCA = S_GAB = $\frac{1}{3}$S_ABC.

Nhận xét. Từ bài tập trên ta có: S_GBC = S_GCA = S_GAB = $\frac{1}{3}$S_ABC điều này giúp ta cảm nhận tại sao có thể đặt thăng bằng miếng bìa hình tam giác trên giá nhọn đặt tại trọng tâm của tam giác đó.

Lời giải:

a) Ta có S_GBC = S_BGM + S_CGM.

Vì G là trọng tâm của tam giác ABC nên GM = $\frac{1}{3}$AM,

suy ra S_BGM = $\frac{1}{3}$S_BAM, S_CGM = $\frac{1}{3}$S_ACM.

Suy ra S_GBC = S_BGM + S_CGM = $\frac{1}{3}$S_BAM + $\frac{1}{3}$S_ACM  = $\frac{1}{3}$(S_BAM + S_ACM) = $\frac{1}{3}$S_ABC.

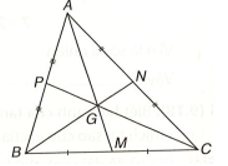
b) Gọi N, P lần lượt là trung điểm của AC và AB.

Tương tự GN = $\frac{1}{3}$BN nên

S_GAC = S_CGN + S_AGN = $\frac{1}{3}$S_BCN + $\frac{1}{3}$S_ABN = $\frac{1}{3}$(S_BCN + S_ABN) = $\frac{1}{3}$S_ABC.

Vì GP = $\frac{1}{3}$CP nên

S_GAB = S_BGP + S_AGP = $\frac{1}{3}$S_BCP + $\frac{1}{3}$S_APC = $\frac{1}{3}$(S_BCP + S_APC) = $\frac{1}{3}$S_ABC.

Vậy S_GBC = S_GCA = S_GAB = $\frac{1}{3}$S_ABC.