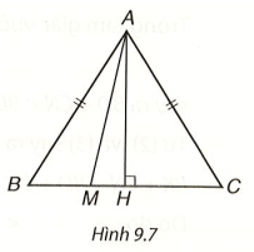
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.7)

Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.7).

Giải vở thực hành Toán 7 Bài 32: Quan hệ giữa đường vuông góc và đường xiên

Bài 2 (9.8) trang 69 vở thực hành Toán lớp 7 Tập 2: Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.7).

a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.

b) Chứng minh rằng với mọi điểm M thì AM < AB.

Lời giải:

a) Kẻ đường cao AH của tam giác ABC, ta có AH là đường vuông góc hạ từ điểm A xuống BC. Gọi M là điểm tùy ý nằm giữa B và C. Nếu M khác H thì AM là đường xiên kẻ từ A đến BC. Do đó theo định lí, AH < AM. Vậy AM nhỏ nhất bằng AH khi M trùng H.

b) M là một điểm nằm giữa B và C. Ta cần chứng minh AM < AB. Muốn vậy, ta xét các trường hợp sau:

Trường hợp 1: Nếu $\widehat{AMB}=90°$, thì AM là đường vuông góc, còn AB là đường xiên kẻ từ A xuống BC theo định lí về đường vuông góc và đường xiên, ta có AM < AB.

Trường hợp 2: Nếu $\widehat{AMB}$ là góc tù thì trong tam giác AMB, góc AMB lớn nhất nên AM < AB.

Trường hợp 3: Nếu $\widehat{AMB}$ là góc nhọn thì góc AMC kề bù với nó nên $\widehat{AMC}$ là góc tù.

Trong tam giác AMC, góc AMC lớn nhất. Do đó AM < AC = AB.