Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM

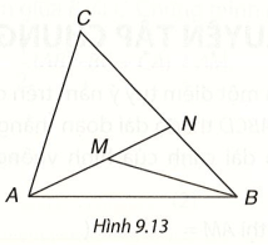
Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.13).

Giải vở thực hành Toán 7 Bài 33: Quan hệ giữa ba cạnh của một tam giác

Bài 3 (9.12) trang 73 vở thực hành Toán lớp 7 Tập 2: Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.13).

a) So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB.

b) So sánh NA với CA + CN, từ đó suy ra NA + NB < CA + CB.

c) Chứng minh MA + MB < CA + CB.

Lời giải:

a) Trong tam giác MNB ta có MB < MN + NB, do đó

MA + MB < MA + MN + NB = NA + NB (vì MA + MN = NA).

b) Trong tam giác ACN ta có NA < CA + CN, do đó

NA + NB < CA + CN + NB = CA + CB (vì CN + NB = CB).

c) Từ a) và b) ta có          MA + MB < NA + NB,

                                        NA + NB < CA + CB.

Suy ra MA + MB < NA + NB < CA + CB.