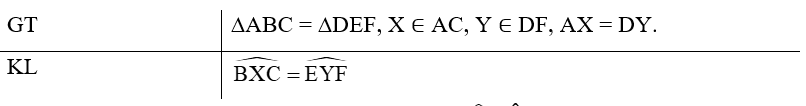Giải Vở thực hành Toán 7 trang 65 Tập 1 Kết nối tri thức
Với Giải VTH Toán 7 trang 65 Tập 1 trong Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Vở thực hành Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 65.
Giải Vở thực hành Toán 7 trang 65 Tập 1 Kết nối tri thức
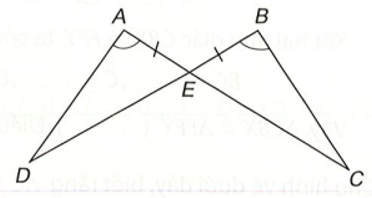
Bài 3 (4.14) trang 65 vở thực hành Toán lớp 7 Tập 1: Chứng minh rằng hai tam giác ADE và BCE trong hình dưới đây bằng nhau.
Lời giải:
∆ADE và ∆BCE có:
(theo giả thiết).
(2 góc đối đỉnh).
EA = EB (theo giả thiết).
Do đó ∆ADE = ∆BCE (g – c – g).
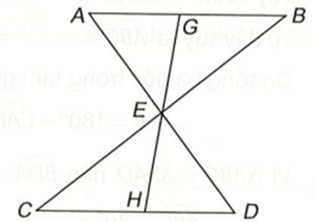
Bài 4 (4.15) trang 65 vở thực hành Toán lớp 7 Tập 1: Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H thẳng hàng. Chứng minh rằng:
a) b) EG = EH.
Lời giải:
a) ∆ABE và ∆DCE có:
(chứng minh trên).
AB = CD (theo giả thiết).
(chứng minh trên).
Do đó ∆ABE = ∆DCE (g – c – g).
b) ∆AGE và ∆DHE có:
(hai góc so le trong).
AE = DE (∆ABE = ∆DCE).
(chứng minh trên).
Do đó ∆AGE = ∆DHE (g – c – g). Từ đây suy ra EG = EH (2 cạnh tương ứng).
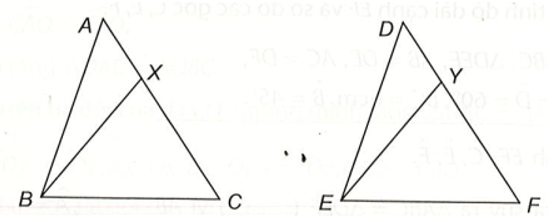
Bài 5 trang 65 vở thực hành Toán lớp 7 Tập 1: Cho tam giác ABC bằng tam giác DEF. Trên các cạnh AC và DF lấy các điểm X, Y sao cho AX = DY. Chứng minh .
Lời giải:
Vì ∆ABC = ∆DEF nên ta có: AC = DF, BC = EF, . Từ đây suy ra
CX = AC – AX = DF – DY = FY.
Xét tam giác CBX và FEY, ta có:
BC = FE, , CX = FY (theo chứng minh trên)
Vậy ∆CBX = ∆FEY (c – g – c). Điều này kéo theo rằng .
Lời giải Vở thực hành Toán lớp 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Kết nối tri thức hay khác: