Giải Vở thực hành Toán 7 trang 66 Tập 1 Kết nối tri thức

---

Với Giải VTH Toán 7 trang 66 Tập 1 trong Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Vở thực hành Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 66.

Giải Vở thực hành Toán 7 trang 66 Tập 1 Kết nối tri thức

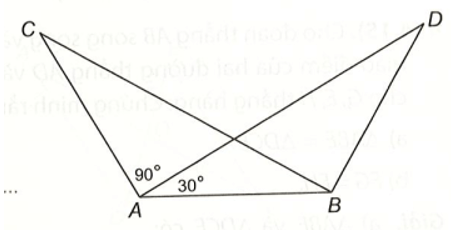
Bài 6 trang 66 vở thực hành Toán lớp 7 Tập 1: Cho hình vẽ dưới đây, biết rằng AC = BD, BC = AD, $\widehat{CAD}=90°$, $\widehat{DAB}=30°$.

Chứng minh rằng ∆ABC = ∆BDA.

Lời giải:

Theo hình vẽ, ta có:

$\widehat{CAB}=\widehat{CAD}+\widehat{DAB}=90°+30°=120°$

Hai tam giác ABC và BAD, có:

AC = BD, BC = AD (theo giả thiết), AB là cạnh chung

Vậy ∆ABC = ∆BAD (c – c – c)

Từ đây suy ra $\widehat{ABC}=\widehat{BAD}=30°$, $\widehat{ABD}=\widehat{BAC}=120°$

Do tổng ba góc trong tam giác ABC bằng 180° nên ta có:

$\widehat{ACB}=180°-\widehat{CAB}-\widehat{ABC}=180°-120°-30°=30°$

Vì ∆ABC = ∆BAD nên $\widehat{BDA}=\widehat{BCA}=30°$

Hai tam giác ABC và BDA, có:

$\widehat{ABC}=30°=\widehat{ADB}$ (theo chứng minh trên)

BC = AD (theo giả thiết)

$\widehat{ACB}=30°=\widehat{BAD}$ (theo chứng minh trên)

Vậy ∆ABC = ∆BDA.

Bài 1 (4.16) trang 66 vở thực hành Toán lớp 7 Tập 1: Cho hai tam giác ABC và DEF thỏa mãn AB = DE, AC = DF, $\widehat{BAC}=\widehat{E\text{D}F}=60°,$ BC = 6 cm, $\widehat{ABC}=45°.$ Tính độ dài cạnh EF và số đo các góc C, E, F.

Lời giải:

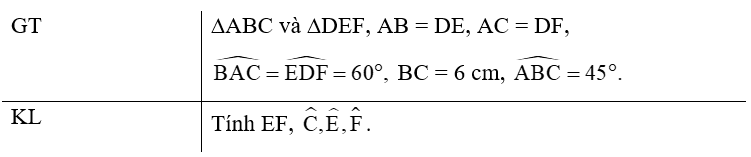
Từ giả thiết suy ra ∆ABC = ∆DEF (c – g – c) vì AB = DE, $\hat{A}=\hat{\text{D}}=60°,$ AC = DF (theo giả thiết). Do các cạnh tương ứng của hai tam giác bằng nhau là bằng nhau nên ta có:

EF = BC = 6cm, $\hat{E}=\hat{B}=45°$, $\hat{F}=\hat{C}$

Do tổng ba góc trong tam giác ABC bằng 180° nên:

$\hat{C}=180°-\hat{A}-\hat{B}=180°-60°-45°=75°$, suy ra $\hat{F}=\hat{C}=75°$.

Kết luận EF = 6 cm, $\hat{C}=75°$, $\hat{E}=45°$, $\hat{F}=75°$.

Lời giải Vở thực hành Toán lớp 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 63 Tập 1

• Giải VTH Toán 7 trang 64 Tập 1

• Giải VTH Toán 7 trang 65 Tập 1

• Giải VTH Toán 7 trang 67 Tập 1

• Giải VTH Toán 7 trang 68 Tập 1