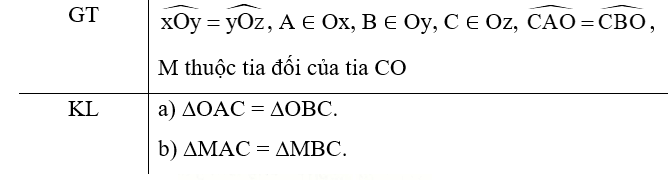Giải Vở thực hành Toán 7 trang 67 Tập 1 Kết nối tri thức

---

Với Giải VTH Toán 7 trang 67 Tập 1 trong Luyện tập chung trang 66, 67, 68 Vở thực hành Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 67.

Giải Vở thực hành Toán 7 trang 67 Tập 1 Kết nối tri thức

Bài 2 (4.17) trang 67 vở thực hành Toán lớp 7 Tập 1: Cho hai tam giác ABC và DEF thỏa mãn AB = DE, $\hat{B}=\hat{E}=70°,\hat{A}=\hat{D}=60°,$ AC = 6 cm. Hãy tính DF.

Lời giải:

Từ giả thiết suy ra ∆ABC = ∆DEF (g – c – g), vì AB = DE, $\hat{B}=\hat{E}=70°,\hat{A}=\hat{D}=60°$ (theo giả thiết). Do các cạnh tương ứng của hai tam giác bằng nhau là bằng nhau nên ta có DF = AC = 6 cm.

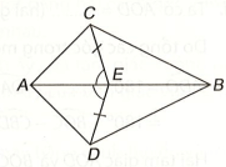
Bài 3 (4.18) trang 67 vở thực hành Toán lớp 7 Tập 1: Cho năm điểm A, B, C, D, E thỏa mãn EC = ED và $\widehat{A\text{E}C}=\widehat{A\text{ED}}$ như hình vẽ dưới đây. Chứng minh rằng:

a) ∆AEC = ∆AED;

b) ∆ABC = ∆ABD.

Lời giải:

a) Xét hai tam giác AEC và AED, ta có:

EC = ED, $\widehat{AEC}=\widehat{AED}$ (theo giả thiết), AE là cạnh chung.

Vậy ∆AEC = ∆AED (c – g – c).

b) Xét hai tam giác ABC và ABD, ta có:

AC = AD, $\widehat{CAB}=\widehat{DAB}$ (vì ∆AEC = ∆AED), AB là cạnh chung.

Vậy ∆ABC = ∆ABD (c – g – c).

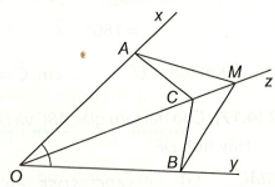
Bài 4 (4.19) trang 67 vở thực hành Toán lớp 7 Tập 1: Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho $\widehat{CAO}=\widehat{CBO}.$

a) Chứng minh rằng ∆OAC = ∆OBC.

b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng ∆MAC = ∆MBC.

Lời giải:

a) Xét hai tam giác OAC và OBC, ta có:

$\widehat{COA}=\widehat{COB}$ (OC là tia phân giác của góc AOB);

OC là cạnh chung;

$\widehat{ACO}=180°-\widehat{CAO}-\widehat{COA}$

$=180°-\widehat{CBO}-\widehat{COB}=\widehat{BCO}$

Vậy ∆OAC = ∆OBC (g – c – g).

b) Xét hai tam giác MAC và MBC có:

C A= CB (do ∆OAC = ∆OBC),

$\widehat{MCA}=180°-\widehat{ACO}=180°-\widehat{BCO}=\widehat{MCB}$ (do ∆OAC = ∆OBC),

MC là cạnh chung.

Vậy ∆MAC = ∆MBC (c – g – c).

Lời giải Vở thực hành Toán lớp 7 Luyện tập chung trang 66, 67, 68 Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 66 Tập 1

• Giải VTH Toán 7 trang 68 Tập 1