Giải Vở thực hành Toán 7 trang 68 Tập 1 Kết nối tri thức

Với Giải VTH Toán 7 trang 68 Tập 1 trong Luyện tập chung trang 66, 67, 68 Vở thực hành Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong VTH Toán 7 trang 68.

Giải Vở thực hành Toán 7 trang 68 Tập 1 Kết nối tri thức

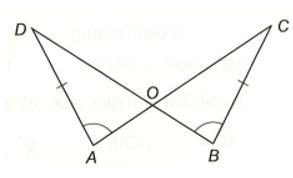
Bài 5 trang 68 vở thực hành Toán lớp 7 Tập 1: Cho hình vẽ dưới dây. Biết rằng AD = BC, $\widehat{DAC}=\widehat{CBD}$, O là giao điểm của AC và BD. Chứng minh rằng AO = BO.

Lời giải:

Ta có: $\widehat{AOD}=\widehat{BOC}$ (hai góc đối đỉnh)

Do tổng các góc trong mỗi tam giác ADO và BCO bằng 180° nên ta có:

$\widehat{ADO}=180°-\widehat{AOD}-\widehat{DAO}=180°-\widehat{BOC}-\widehat{CBO}=\widehat{BCO}$.

Hai tam giác AOD và BOC có:

$\widehat{ADO}=\widehat{BCO}$ (theo chứng minh trên)

AD = BC (theo giả thiết)

$\widehat{DAO}=\widehat{DAC}=\widehat{CBD}=\widehat{CBO}$ (theo giả thiết).

Vậy tam giác ∆AOD = ∆BOC (g – c – g).

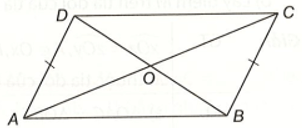
Bài 6 trang 68 vở thực hành Toán lớp 7 Tập 1: Cho hình vẽ đưới đây. Biết đường thẳng AD song song với đường thẳng BC, AD = BC. Chứng minh rằng AB song song với CD.

Lời giải:

Gọi O là giao điểm của AC và BD

Hai tam giác AOD và BOC có:

$\widehat{ADO}=\widehat{CBO}$ (hai góc so le trong);

AD = CB (theo giả thiết);

$\widehat{DAO}=\widehat{BCO}$ (hai góc so le trong).

Vậy ∆AOD = ∆BOC (g – c – g).

Xét tam giác AOB và tam giác COD, ta có:

OA = OC (vì ∆AOD = ∆BOC)

$\widehat{AOB}=\widehat{COD}$ (hai góc đối đỉnh)

OD = OB (vì ∆AOD = ∆BOC)

Vậy ∆AOB = ∆COD (c – g – c)

Suy ra $\widehat{OAB}=\widehat{OCD}$ (cặp góc tương ứng), và do đó AB song song với CD.

Lời giải Vở thực hành Toán lớp 7 Luyện tập chung trang 66, 67, 68 Kết nối tri thức hay khác:

• Giải VTH Toán 7 trang 66 Tập 1

• Giải VTH Toán 7 trang 67 Tập 1