Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó

Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó.

Giải vở thực hành Toán 9 Bài 14: Cung và dây của một đường tròn - Kết nối tri thức

Bài 1 trang 102 VTH Toán 9 Tập 1: Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó.

Chứng minh rằng khoảng cách từ M đến AB không lớn hơn $\frac{A B}{2} .$

Lời giải:

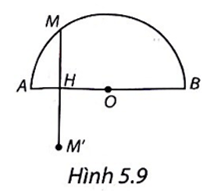
(H.5.9)

Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó

Gọi H là chân đường cao hạ từ M xuống AB.

Khi đó, độ dài đoạn MH là khoảng cách từ M đến AB.

Gọi M' là điểm đối xứng với M qua AB. Khi đó, H là trung điểm của MM', tức là MH = HM'.

Mặt khác, do AB là đường kính của đường tròn nên M' thuộc đường tròn (O).

Suy ra MM' là dây cung của đường tròn.

Do đó $M M^{'} \leq A B,$ hay 2MH ≤ AB, suy ra $M H \leq \frac{A B}{2} .$

Vậy khoảng cách từ M đến AB không lớn hơn $\frac{A B}{2} .$

Lời giải vở thực hành Toán 9 Bài 14: Cung và dây của một đường tròn hay khác: