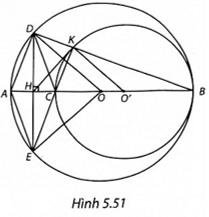
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB.
Giải vở thực hành Toán 9 Bài tập cuối chương 5 - Kết nối tri thức
Bài 10 trang 126 VTH Toán 9 Tập 1: Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB.
a) Xác định vị trí tương đối của hai đường tròn (O) và (O').
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
c) Gọi K là giao điểm của DB và đường tròn (O'). Chứng minh ba điểm E, C, K thẳng hàng.
d) Chứng minh HK là tiếp tuyến của đường tròn (O').
Lời giải:
(H.5.51)
a) Gọi R, r lần lượt là bán kính của hai đường tròn (O) và (O').
Ta có OO' = R – r nên hai đường tròn (O) và (O') tiếp xúc trong với nhau.
b) Tam giác ODE cân tại O (OD = OE = R) có OH là đường cao nên đồng thời là đường trung tuyến của ∆ODE, hay DH = HE.
Tứ giác ADCE có hai đường chéo AC và DE cắt nhau tại H là trung điểm mỗi đường nên ADCE là hình bình hành. Lại có AC ⊥ DE tại H, suy ra ADCE là hình thoi.
c) Tam giác KCB có đường trung tuyến KO' và KO' = CO' = BO' nên tam giác KCB là tam giác vuông tại K, suy ra hay KC ⊥ KB. (1)
Tương tự, ta có hay DA ⊥ DB. (2)
Từ (1) và (2) suy ra KC // AD.
Lại có EC // AD (vì ADCE là hình thoi), do đó ba điểm E, C, K thẳng hàng.
d) Xét tam giác DEK vuông tại K có KH là đường trung tuyến nên KH = DH = EH.
Do đó tam giác KHE cân tại H, suy ra
Lại có, ∆O'CK cân tại O' nên
Mặt khác (hai góc đối đỉnh).
Tam giác HEC vuông tại H nên
Suy ra hay
Do đó HK ⊥ O'K.
Vậy HK là tiếp tuyến của đường tròn (O').
Lời giải vở thực hành Toán 9 Bài tập cuối chương 5 hay khác: