Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Một đường thẳng d đi qua A
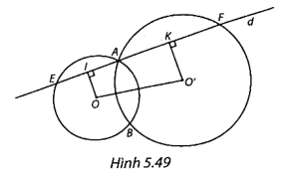
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Một đường thẳng d đi qua A cắt (O) tại E và cắt (O') tại F (E và F khác A). Biết điểm A nằm trong đoạn EF. Gọi I và K lần lượt là trung điểm của AE và AF (H.5.49).
Giải vở thực hành Toán 9 Bài tập cuối chương 5 - Kết nối tri thức
Bài 9 trang 125 VTH Toán 9 Tập 1: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Một đường thẳng d đi qua A cắt (O) tại E và cắt (O') tại F (E và F khác A). Biết điểm A nằm trong đoạn EF. Gọi I và K lần lượt là trung điểm của AE và AF (H.5.49).
a) Chứng minh rằng tứ giác OO'KI là một hình thang vuông.
b) Chứng minh rằng
C) Khi d ở vị trí nào (d vẫn qua A) thì OO'KI là một hình chữ nhật?
Lời giải:
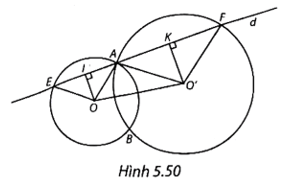
(H.5.50)
a) ∆AOE là tam giác cân tại O (OA = OE) có OI là đường trung tuyến (vì I là trung điểm của AE) nên OI cũng là đường cao, tức là hay OI ⊥ AI.
Tương tự, đối với tam giác AO'F, ta có hay O'K ⊥ KF.
Do đó OI // O'K (cùng vuông góc với d).
Tứ giác OO'KI có OI // O'K và nên OO'KI là hình thang vuông.
b) Theo đề bài, EI = IA và AK = KF nên ta có EA = 2IA và AF = 2AK.
Ta có: EF = EA + AF = 2IA + 2AK = 2(IA + AK) = 2IK. Do đó
c) Khi d đi qua A thì tứ giác OO'KI luôn là hình thang vuông.
Nếu hình thang vuông đó là hình chữ nhật thì IK // OO', hay d // OO'.
Ngược lại, nếu d // OO' thì IK // OO' nên OO'KI là hình chữ nhật.
Vậy để tứ giác OO'KI là hình chữ nhật thì d // OO'.
Lời giải vở thực hành Toán 9 Bài tập cuối chương 5 hay khác: