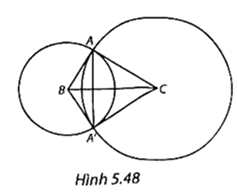
Cho tam giác vuông ABC ( góc A vuông ). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A'
Cho tam giác vuông ABC ( vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A'. Chứng minh rằng:
Giải vở thực hành Toán 9 Bài tập cuối chương 5 - Kết nối tri thức
Bài 8 trang 124 VTH Toán 9 Tập 1: Cho tam giác vuông ABC ( vuông). Vẽ hai đường tròn (B; BA) và (C; CA) cắt nhau tại A và A'. Chứng minh rằng:
a) BA và BA' là hai tiếp tuyến cắt nhau của đường tròn (C; CA);
b) CA và CA' là hai tiếp tuyến cắt nhau của đường tròn (B; BA).
Lời giải:
(H.5.48)
a) Tam giác ABC vuông tại A nên AB ⊥ AC, mà A ∈ (C; CA) do đó BA là tiếp tuyến của đường tròn (C; CA).
Hai tam giác ABC và A'BC có:
BC là cạnh chung;
AB = A'B (cùng bằng bán kính đường tròn (B; BA));
AC = A'C (cùng bằng bán kính đường tròn (C; CA)).
Do đó ∆ABC = ∆A'BC (c.c.c), suy ra hay BA' ⊥ A'C.
Mặt khác, A' ∈ (C; CA) nên BA' là tiếp tuyến của đường tròn (C; CA).
Vậy BA và BA' là hai tiếp tuyến của đường tròn (C; CA) cắt nhau tại C.
b) Ta có CA ⊥ AB và A ∈ (B; BA) nên CA là tiếp tuyến của đường tròn (B; BA).
Tương tự, CA' là tiếp tuyến của đường tròn (B; BA).
Vậy CA và CA' là hai tiếp tuyến của đường tròn (B; BA) cắt nhau tại B.
Lời giải vở thực hành Toán 9 Bài tập cuối chương 5 hay khác: