Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X như hình bên

Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X như hình bên. Tính số đo của góc AXB, biết rằng và

Giải vở thực hành Toán 9 Bài 27: Góc nội tiếp - Kết nối tri thức

Bài 3 trang 88 VTH Toán 9 Tập 2: Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X như hình bên. Tính số đo của góc AXB, biết rằng $\widehat{ADB}=30°$ và $\widehat{DBC}=50°.$

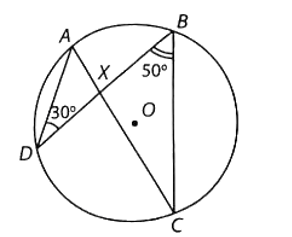
Lời giải:

Do $\widehat{DAC}$ và $\widehat{DBC}$ là hai góc nội tiếp cùng chắn một cung của (O) nên $\widehat{DAC}=\widehat{DBC}=50°.$

Vì tổng ba góc trong một tam giác bằng 180° và góc AXB kề bù với góc AXD nên $\widehat{AXB}=180°-\widehat{AXD}=\widehat{DAX}+\widehat{ADX}=80°.$

Lời giải vở thực hành Toán 9 Bài 27: Góc nội tiếp hay khác:

• Câu 1 trang 86 VTH Toán 9 Tập 2: Chọn phương án đúng. Cho tam giác nhọn ABC nội tiếp đường tròn (O). ...

• Câu 2 trang 87 VTH Toán 9 Tập 2: Chọn phương án đúng. Cho tam giác ABC nội tiếp đường tròn (O). Biết $\widehat{BAC}=100°,$...

• Bài 1 trang 87 VTH Toán 9 Tập 2: Những khẳng định nào sau đây là đúng? Hai góc nội tiếp bằng nhau thì chắn cùng một cung...

• Bài 2 trang 87 VTH Toán 9 Tập 2: Cho các điểm như hình bên. Tính số đo các góc của tam giác ABC...

• Bài 4 trang 88 VTH Toán 9 Tập 2: Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) như hình bên....

• Bài 5 trang 88 VTH Toán 9 Tập 2: Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A) ...

• Bài 6 trang 89 VTH Toán 9 Tập 2: Trên sân bóng, khi quả bóng được đặt tại điểm phạt đền thì có góc sút bằng 36° và quả bóng cách mỗi cọc gôn 11,6 m ...

• Bài 7 trang 89 VTH Toán 9 Tập 2: Cho các điểm A, B, C, D trên đường tròn (O) như hình bên. Biết rằng CD là đường kính của (O) ...

• Bài 8 trang 90 VTH Toán 9 Tập 2: Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC của tam giác ABC lần lượt tại F và E....