Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC

❮ Bài trước Bài sau ❯

Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC của tam giác ABC lần lượt tại F và E.

Giải vở thực hành Toán 9 Bài 27: Góc nội tiếp - Kết nối tri thức

Bài 8 trang 90 VTH Toán 9 Tập 2: Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC của tam giác ABC lần lượt tại F và E.

a) Cho BE cắt CF tại H. Chứng minh rằng AH vuông góc với BC.

b) Chứng minh rằng EF song song với BC.

Lời giải:

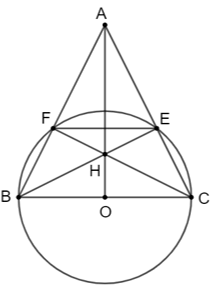
Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC

a) Gọi (O) là đường tròn đường kính BC.

Vì $\hat{B E C}$ và $\hat{C F B}$ là hai góc nội tiếp của (O) chắn nửa đường tròn nên $\hat{B E C} = \hat{C F B} = 90 ° .$ Suy ra BE ⊥ AC, CF ⊥ AB.

Do đó H là trực tâm của tam giác ABC.

Vì vậy AH vuông góc với BC.

b) Vì $\hat{E F C}$ và $\hat{E B C}$ là hai góc nội tiếp của (O) cùng chắn cung $\overset{⏜}{C E}$ nên $\hat{E F C} = \hat{E B C} .$ (1)

Mặt khác, tam giác ABC cân tại A và các tam giác BCF, CBE lần lượt vuông tại F và E nên: $\hat{E B C} = 90 ° - \hat{E C B} = 90 ° - \hat{F B C} = \hat{F C B} .$ (2)

Từ (1) và (2) suy ra $\hat{E F C} = \hat{F C B} .$ Do đó EF // BC (hai góc so le trong).

Lời giải vở thực hành Toán 9 Bài 27: Góc nội tiếp hay khác:

Vở thực hành Toán 9

Cho tam giác nhọn ABC cân tại đỉnh A. Đường tròn đường kính BC cắt các cạnh AB, AC

Giải vở thực hành Toán 9 Bài 27: Góc nội tiếp - Kết nối tri thức

Xem thêm các bài giải vở thực hành Toán lớp 9 Kết nối tri thức hay, chi tiết khác: