Hãy tính độ dài của cạnh của bát giác đều nội tiếp một đường tròn bán kính căn 2 cm

Hãy tính độ dài của cạnh của bát giác đều nội tiếp một đường tròn bán kính cm.

Giải vở thực hành Toán 9 Luyện tập chung trang 106 - Kết nối tri thức

Bài 7 trang 109 VTH Toán 9 Tập 2: Hãy tính độ dài của cạnh của bát giác đều nội tiếp một đường tròn bán kính $\sqrt{2}$ cm.

Lời giải:

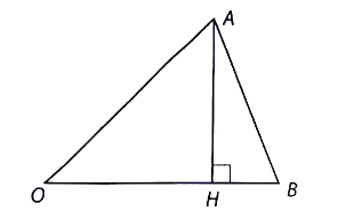
Gọi AB là một cạnh của bát giác đều và (O) là đường tròn ngoại tiếp bát giác đều.

Khi đó OAB là tam giác cân tại O có cạnh bên $O A = O B = \sqrt{2}$ cm và góc ở đỉnh $\hat{A O B} = \frac{360 °}{8} = 45 ° .$

Kẻ đường cao AH của tam giác OAB. Khi đó AHO là tam giác vuông tại H.

Theo định lí Pythagore, ta có OA² = AH² + HO² = 2HA².

Suy ra $H O = A H = \frac{\sqrt{2}}{\sqrt{2}} = 1$ (cm).

Áp dụng hệ thức lượng cho tam giác AHB vuông tại H, ta được:

$A B = \sqrt{A H^{2} + H B^{2}} = \sqrt{A H^{2} + {(O B - H O)}^{2}}$

$= \sqrt{1^{2} + {(\sqrt{2} - 1)}^{2}} = \sqrt{4 - 2 \sqrt{2}}$ (cm)

Lời giải vở thực hành Toán 9 Luyện tập chung trang 106 hay khác: