Cho hai số thực x, y thỏa mãn Gọi M, m lần lượt là giá trị lớn nhất

Câu hỏi:

Cho hai số thực x, y thỏa mãn $x^{2} + y^{2} - 4 x + 6 y + 4 + \sqrt{y^{2} + 6 y + 10} = \sqrt{6 + 4 x - x^{2}}$ Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức $T = |\sqrt{x^{2} + y^{2}} - a|$ . Có bao nhiêu giá trị nguyên thuộc đoạn $[- 10; 10]$ của tham số a để $M \geq 2 m$ ?

A. 17

B. 10

C. 15

D. 18

Trả lời:

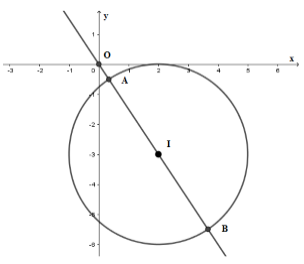
Ta có: $x^{2} + y^{2} - 4 x + 6 y + 4 + \sqrt{y^{2} + 6 y + 10} = \sqrt{6 + 4 x - x^{2}}$

$\Leftrightarrow x^{2} + y^{2} - 4 x + 6 y + 4 + \sqrt{y^{2} + 6 y + 10} - \sqrt{6 + 4 x - x^{2}} = 0$

$\Leftrightarrow x^{2} + y^{2} - 4 x + 6 y + 4 + \frac{(\sqrt{y^{2} + 6 y + 10} - \sqrt{6 + 4 x - x^{2}}) (\sqrt{y^{2} + 6 y + 10} + \sqrt{6 + 4 x - x^{2}})}{\sqrt{y^{2} + 6 y + 10} + \sqrt{6 + 4 x - x^{2}}} = 0$

$\Leftrightarrow x^{2} + y^{2} - 4 x + 6 y + 4 + \frac{y^{2} + 6 y + 10 - 6 - 4 x + x^{2}}{\sqrt{y^{2} + 6 y + 10} + \sqrt{6 + 4 x - x^{2}}} = 0$

$\Leftrightarrow x^{2} + y^{2} - 4 x + 6 y + 4 + \frac{x^{2} + y^{2} - 4 x + 6 y + 4}{\sqrt{y^{2} + 6 y + 10} + \sqrt{6 + 4 x - x^{2}}} = 0$

$\Leftrightarrow (x^{2} + y^{2} - 4 x + 6 y + 4) + (1 + \frac{1}{\sqrt{y^{2} + 6 y + 10} + \sqrt{6 + 4 x - x^{2}}}) = 0$

$\Leftrightarrow x^{2} + y^{2} - 4 x + 6 y + 4 = 0$

(vì $1 + \frac{1}{\sqrt{y^{2} + 6 y + 10} + \sqrt{6 + 4 x - x^{2}}} > 0$ )

$\Leftrightarrow {(x - 2)}^{2} + {(y + 3)}^{2} = 9$

Phương trình $\Leftrightarrow {(x - 2)}^{2} + {(y + 3)}^{2} = 9$ là phương trình đường tròn $(C)$ tâm $I (2; - 3)$ và bán kính R = 3.

Gọi $N (x; y) \in (C)$ ta suy ra $O N = \sqrt{x^{2} + y^{2}}$ suy ra $T = |O N - a|$

Gọi A, B là giao điểm của đường tròn $(C)$ và đường thẳng OI.

Khi đó, $O A = O I - R = \sqrt{13} - 3$ và $O B = O I + R = \sqrt{13} + 3$

Suy ra $\sqrt{13} - 3 \leq \sqrt{x^{2} + y^{2}} \leq \sqrt{13} + 3$

TH1: nếu $\sqrt{13} - 3 \leq a \leq \sqrt{13} + 3$ thì $|\sqrt{x^{2} + y^{2}} - a| \geq 0 \Rightarrow \min T = 0 \Rightarrow M \geq 2 m \Rightarrow a \in \{1; 2; 3; 4; 5; 6\}$

TH2: Nếu $a < \sqrt{13} - 3 \Rightarrow a < \sqrt{13}$ nên $|\sqrt{13} + 3 - a| > |\sqrt{13} - 3 - a|$ , do đó $M = |\sqrt{13} + 3 - a|; m = |\sqrt{13} - 3 - a|$

Vì $M \geq 2 m \Rightarrow |\sqrt{13} + 3 - a| \geq 2 |\sqrt{13} - 3 - a|$

$\Leftrightarrow {(\sqrt{13} - 3 - a)}^{2} - {(2 \sqrt{13} + 6 - 2 a)}^{2} \geq 0 \Leftrightarrow \sqrt{13} + 1 \leq a \leq \sqrt{13} + 9 \Rightarrow a \in \{5; 6; 7; 8; 9; 10\}$

Vậy có 10 giá trị của a thỏa mãn đề bài.

Đáp án cần chọn là: B

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số $y = \frac{x - m^{2} - 2}{x - m}$ trên đoạn $[0; 4]$ bằng – 1.

Xem lời giải »

Câu 2:

Cho f (x) mà đồ thị hàm số $y = f' (x)$ như hình vẽ bên

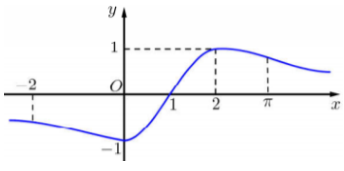
Bất phương trình $f (x) > \sin \frac{π x}{2} + m$ nghiệm đúng với mọi $x \in [- 1; 3]$ khi và chỉ khi:

Xem lời giải »

Câu 3:

Cho $f (x) = \frac{1}{x^{2} - 4 x + 5} - \frac{x^{2}}{4} + x$ . Gọi $M = \max_{x \in [0; 3]} f (x); m = \min_{x \in [0; 3]} f (x)$ . Khi đó $M - m$ bằng:

Xem lời giải »

Câu 4:

Cho hàm số f (x). Biết rằng hàm số $f' (x)$ có đồ thị như hình dưới đây. Trên đoạn $[- 4; 3]$ , hàm số $g (x) = 2 f (x) + {(1 - x)}^{2}$ đạt giá trị nhỏ nhất tại điểm

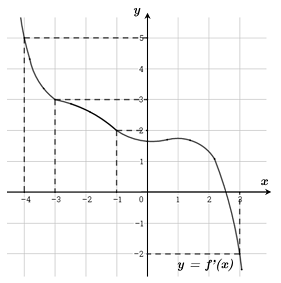
Xem lời giải »

Câu 5:

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình bên:

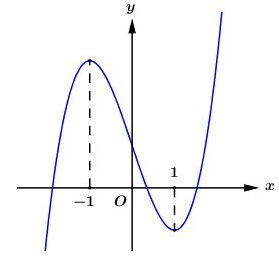
Giá trị nguyên lớn nhất của tham số m để hàm số $y = f (|x| - m)$ đồng biến trên khoảng $(10; + \infty)$ là:

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hai số thực x, y thỏa mãn Gọi M, m lần lượt là giá trị lớn nhất

Xem thêm bài tập Toán có lời giải hay khác: