Bài 3.24 trang 61 Chuyên đề Toán 10

Giải Chuyên đề Toán 10 Bài tập cuối chuyên đề 3

Haylamdo biên soạn và sưu tầm lời giải Bài 3.24 trang 61 Chuyên đề Toán 10 trong Bài tập cuối chuyên đề 3. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

Bài 3.24 trang 61 Chuyên đề Toán 10: Cho hai parabol có phương trình y² = 2px và y = ax² + bx + c (a ≠ 0). Chứng minh rằng nếu hai parabol đó cắt nhau tại bốn điểm phân biệt thì bốn điểm đó cùng nằm trên đường tròn $\left(C\right):x^2+y^2+\left(\frac{b}{a}-2p\right)x-\frac{1}{a}y+\frac{c}{a}=0$.

Lời giải:

+) Xét trường hợp a > 0.

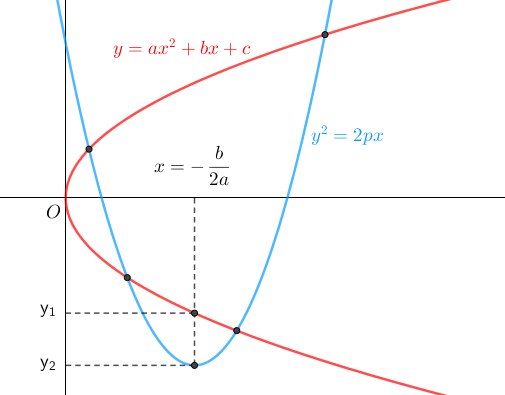
Để hai parabol cắt nhau tại 4 điểm phân biệt thì đỉnh của parabol y = ax² + bx + c phải nằm ở góc phần tư thứ IV (như hình vẽ).

Khi đó ta suy ra b < 0 và phương trình ax² + bx + c có hai nghiệm phân biệt

⇒ b² – 4ac > 0

Xét phương trình đường tròn $\left(C\right):x^2+y^2+\left(\frac{b}{a}-2p\right)x-\frac{1}{a}y+\frac{c}{a}=0.$

có ${\left[\frac{\left(\frac{b}{a}-2p\right)}{2}\right]}^2+{\left[\frac{\frac{1}{a}}{2}\right]}^2-\frac{c}{a}={\left(\frac{b}{2a}-p\right)}^2+{\left(\frac{1}{2a}\right)}^2-\frac{c}{a}$

$=\frac{b^2}{4a^2}-\frac{b}{a}.p+p^2+\frac{1}{4a^2}-\frac{c}{a}$

$=\left(\frac{b^2}{4a^2}-\frac{c}{a}\right)-\frac{b}{a}.p+p^2+\frac{1}{4a^2}$

$=\frac{b^2-4ac}{4a^2}-\frac{b}{a}.p+p^2+\frac{1}{4a^2}$

Vì b < 0 và b² – 4ac > 0 (chứng minh trên) nên $-\frac{b}{a}$.p > 0 và $\frac{b2–4ac}{4a^2}$ > 0

Do đó ${\left[\frac{\left(\frac{b}{a}-2p\right)}{2}\right]}^2+{\left[\frac{\frac{1}{a}}{2}\right]}^2-\frac{c}{a}>0.$

Vậy (C) đúng là phương trình một đường tròn.

+) Trường hợp a < 0: Chứng minh tương tự ta được (C) đúng là phương trình một đưởng tròn.

+) Giờ ta chứng minh bốn giao điểm của hai parabol nằm trên đường tròn này. Thật vậy:

Nếu điểm M(x; y) là giao điểm của hai parabol trên thì ta có:

y² = 2px và y = ax² + bx + c ⇒ y² – 2px = 0 và ax² + bx + c – y = 0

⇒ y² – 2px = 0 và $x^2+\frac{b}{a}x+\frac{c}{a}-\frac{y}{a}=0$

⇒ $\left(x^2+\frac{b}{a}x+\frac{c}{a}-\frac{y}{a}\right)+\left(y^2-2px\right)=0$

⇒ $x^2+y^2+\left(\frac{b}{a}x-2px\right)-\frac{y}{a}+\frac{c}{a}=0$

⇒ $x^2+y^2+\left(\frac{b}{a}-2p\right)x-\frac{1}{a}y+\frac{c}{a}=0.$

Do đó M thuộc đường tròn (C). Vậy bốn giao điểm của parabol đều nằm trên (C).