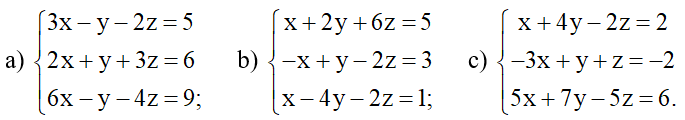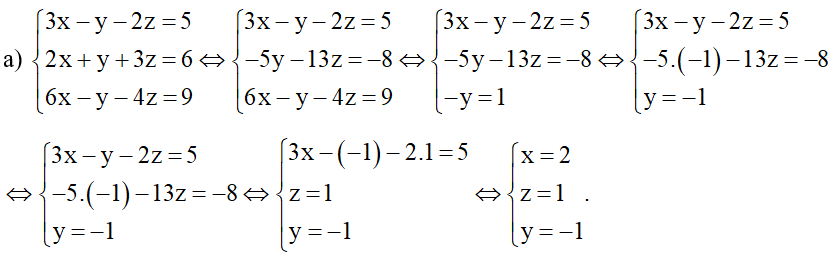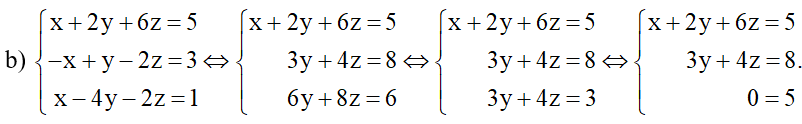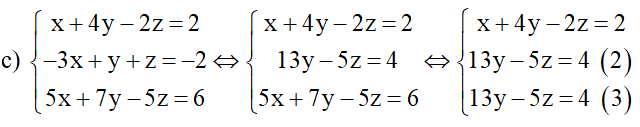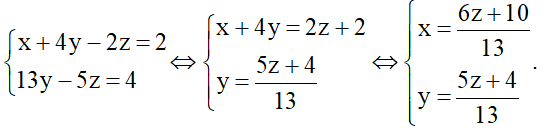Bài 3 trang 11 Chuyên đề Toán 10

Giải Chuyên đề Toán 10 Bài 1: Hệ phương trình bậc nhất ba ẩn

Haylamdo biên soạn và sưu tầm lời giải Bài 3 trang 11 Chuyên đề Toán 10 trong Bài 1: Hệ phương trình bậc nhất ba ẩn. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

Bài 3 trang 11 Chuyên đề Toán 10: Giải hệ phương trình:

Lời giải:

Vậy hệ phương trình đã cho có nghiệm (x; y; z) = (2; –1; 1)

Phương trình thứ ba của hệ vô nghiệm. Vậy hệ đã cho vô nghiệm.

Hai phương trình (2) và (3) tương đương. Khi đó, hệ phương trình đưa về:

Đặt z = t với t là số thực bất kì, ta có:

$x=\frac{6t+10}{13},y=\frac{5t+4}{13}.$

Vậy hệ phương trình đã cho có vô số nghiệm (x ; y ; z) = $\left(\frac{6t+10}{13};\frac{5t+4}{13};t\right)$với t là số thực bất kì.