Đề cương ôn tập Giữa kì 1 Toán 9 Cánh diều

---

Haylamdo biên soạn và sưu tầm bộ đề cương ôn tập Giữa kì 1 Toán 9 Cánh diều với bài tập trắc nghiệm, tự luận đa dạng có lời giải chi tiết giúp học sinh nắm vững được kiến thức cần ôn tập để đạt điểm cao trong bài thi Toán 9 Giữa kì 1.

Đề cương ôn tập Giữa kì 1 Toán 9 Cánh diều

Xem thử

Chỉ từ 80k mua trọn bộ đề cương ôn tập Toán 9 Giữa kì 1 Cánh diều bản word có lời giải chi tiết, trình bày đẹp mắt, dễ dàng chỉnh sửa:

• B1: gửi phí vào tk: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
• B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi

Đề cương ôn tập Toán 9 Giữa kì 1 Cánh diều gồm hai phần: Nội dung ôn tập và Bài tập ôn luyện, trong đó:

- 42 bài tập trắc nghiệm;

- 27 bài tập tự luận;

PHẦN I. TÓM TẮT NỘI DUNG KIẾN THỨC

A. Số

Chương I. Phương trình và hệ phương trình bậc nhất

– Phương trình quy về phương trình bậc nhất một ẩn

– Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

– Giải hệ hai phương trình bậc nhất hai ẩn

– Giải bài toán bằng cách lập hệ phương trình

Chương II. Phương trình và bất phương trình bậc nhất một ẩn

– Bất đẳng thức và tính chất

– Bất phương trình bậc nhất một ẩn

B. Hình học

Chương IV. Hệ thức lượng trong tam giác vuông

– Tỉ số lượng giác của góc nhọn

– Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

PHẦN II. MỘT SỐ CÂU HỎI, BÀI TẬP THAM KHẢO

A. Bài tập trắc nghiệm

1. Câu trắc nghiệm nhiều phương án lựa chọn

Khoanh tròn chữ cái đứng trước câu trả lời đúng duy nhất

Câu 1. Tổng các nghiệm của phương trình (3x + 1)(2 – 3x) là

A. $\frac{1}{3}$.

B. $-\frac{1}{3}$.

C. 1.

D. –1.

Câu 2. Điều kiện xác định của phương trình $\frac{4x-1}{x+2}+1=\frac{3}{x-3}$ là:

A. x ≠ 2 và x ≠ 3.

B. x ≠ –2 và x ≠ 3.

C. x ≠ 2 và x ≠ –3.

D. x ≠ –2 và x ≠ –3.

Câu 3. Số nghiệm của phương trình $\frac{4}{x\left(x-1\right)}+\frac{3}{x}=\frac{4}{x-1}$ là

A. 0.

B. 1.

C. 2.

D. 3.

Câu 4. Phương trình nào sau đây là phương trình bậc nhất hai ẩn?

A.  x² + 2y = 3.

B. $x+\frac{1}{y}=5$.

C.  3x – 4y + 7 = 0.

D.  xy + 2 = 0.

Câu 5. Phương trình nào dưới đây nhận cặp số (2; –1)  làm nghiệm?

A. x + 2y = 0.

B. 2x – y = 3.

C. x – y = 1.

D. 3x + y = 5.

Câu 6. Khẳng định nào sau đây là đúng về đường thẳng biểu diễn tất cả các nghiệm của phương trình  x – 2y = 0?

A. Vuông góc với trục tung.

B. Vuông góc với trục hoành.

C. Đi qua gốc tọa độ.

D. Đi qua điểm A(1; 2).

Câu 7. Cho phương trình 2x – 3y = 6. Nghiệm tổng quát của phương trình trên là:

A. $\left(3+\frac{3}{2}y;y\right)$ với y ∈ ℝ tùy ý.

B. $\left(x;\frac{2}{3}x+2\right)$ với x ∈ ℝ tùy ý.

C. $\left(3-\frac{3}{2}y;y\right)$ với y ∈ ℝ tùy ý.

D. $\left(x;\frac{3}{2}-3x\right)$ với x ∈ ℝ tùy ý.

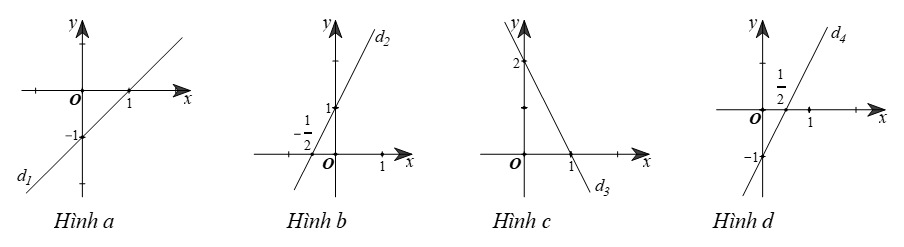
Câu 8. Cho các đường thẳng được biểu diễm trên mặt phẳng tọa độ Oxy như sau:

Tất cả các nghiệm của phương trình 2x – y = 1 được biểu diễn bởi đường thẳng nào?

A. d₁.

B. d₂.

C. d₃.

D. d₄.

Câu 9. Cặp số $\left(\frac{8}{5};-\frac{9}{5}\right)$ là nghiệm của hệ phương trình nào sau đây?

A. $\left\{\begin{array}{l}x+2y=5\\ 2x-y=1.\end{array}\right.$

B. $\left\{\begin{array}{l}3x-2y=4\\ x+y=5.\end{array}\right.$

C. $\left\{\begin{array}{l}x-y=2\\ 2x+3y=9.\end{array}\right.$

D. $\left\{\begin{array}{l}4x+3y=1\\ 2x-y=5.\end{array}\right.$

Câu 10. Giá trị của a và b để cặp số (–2; 3) là nghiệm của hệ phương trình $\left\{\begin{array}{l}ax+3y=1\\ x+by=-2\end{array}\right.$ là

A. a = 4; b = 0.

B. a = 2; b = 2.

C. a = 0; b = 4.

D. a = –2; b = –2.

................................

................................

................................

B. Bài tập tự luận

1. Số

Dạng 1. Giải phương trình và bất phương trình

Bài 1. Giải các phương trình sau:

a) (2x + 1)(x – 2) = 0.

b) $\left(\frac{2}{3}x-5\right)\left(2-3x\right)=0$.

c) x² + 3x = 0.

d) x² – 9 = 3(x + 3).

e) (x – 3)² = (2x – 1)².

f) 3x² – 11x + 6 = 0.

g) $\frac{x+6}{x+5}+\frac{3}{2}=2$.

h) $\frac{2}{x-2}+\frac{3}{3-x}=\frac{3x-20}{\left(x-3\right)\left(x-2\right)}$.

i) $\frac{1}{x-1}-\frac{4x}{x^3-1}=\frac{x}{x^2+x+1}$.

j) $\frac{x-1}{x+3}-\frac{x}{x-3}=\frac{7x-3}{9-x^2}$.

Bài 2. Giải các bất phương trình sau:

a) 0,5x – 6 ≤ 0.

b) 2x + 5 < 3x – 4.

c) –3x + 5 ≥ –4x + 3.

d) $\frac{2x-5}{18}>\frac{4x+3}{10}$.

e) $\frac{8-3x}{2}-x<5$.

f) $\frac{x\left(x+1\right)}{12}-\frac{x-1}{8}\le \frac{2x^2+3}{24}+\frac{5x}{6}$.

g) –5(x – 2) + 2(x + 3) ≥ 7.

h) 2x(6x – 1) ≤ (3x – 2)(4x + 3).

i) (4x – 1)² – 2 ≥ 16(x – 1)(x + 1) + 2x.

Dạng 2. Giải hệ phương trình

Bài 3. Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{array}{c}x-2y=1\\ 3x+2y=3.\end{array}\right.$

b) $\left\{\begin{array}{c}8x+3y=5\\ 4x+y=2.\end{array}\right.$

c) $\left\{\begin{array}{c}-2x-3y=9\\ -x-y=2.\end{array}\right.$

Bài 4. Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{array}{c}3x+y=3\\ 2x-y=7.\end{array}\right.$

b) $\left\{\begin{array}{c}2x+5y=8\\ 2x-3y=0.\end{array}\right.$

c) $\left\{\begin{array}{c}-5x+2y=4\\ 6x-3y=-7.\end{array}\right.$

Bài 5. Giải các hệ phương trình sau:

a) $\left\{\begin{array}{c}\left(3x+2\right)\left(2y-3\right)=6xy\\ \left(4x+5\right)\left(y-5\right)=4xy.\end{array}\right.$

b) $\left\{\begin{array}{c}\frac{1}{x}-\frac{2}{y}=-1\\ \frac{2}{x}+\frac{1}{y}=3.\end{array}\right.$

c) $\left\{\begin{array}{c}\left|x+2\right|+4\left|y-1\right|=5\\ 3\left|x+2\right|-2\left|y-1\right|=1.\end{array}\right.$

d) $\left\{\begin{array}{c}\left|x+2\right|+\frac{4}{\left|2y-1\right|}=5\\ 3\left|x+2\right|-\frac{2}{\left|2y-1\right|}=1.\end{array}\right.$

................................

................................

................................

Xem thử