200 Đề thi Toán 9 năm 2024 (có đáp án)
Haylamdo biên soạn và sưu tầm bộ 200 Đề thi Toán 9 năm 2024 mới nhất đầy đủ Học kì 1 và Học kì 2 gồm đề thi giữa kì, đề thi học kì có đáp án chi tiết, cực sát đề thi chính thức giúp học sinh ôn luyện & đạt điểm cao trong các bài thi Toán 9.
Đề thi Toán 9 năm 2024 (có đáp án)
Đề thi Toán 9 Kết nối tri thức
Đề thi Toán 9 Chân trời sáng tạo
Đề thi Toán 9 Cánh diều
Đề cương ôn tập Toán 9
Đề cương Toán 9 Kết nối tri thức
Đề cương Toán 9 Chân trời sáng tạo
Đề cương Toán 9 Cánh diều
Lưu trữ: Đề thi Toán 9 (sách cũ)
Xem thử Đề Toán 9 GK1 Xem thử Đề Toán 9 CK1 Xem thử Đề Toán 9 GK2 Xem thử Đề Toán 9 CK2
Chỉ từ 150k mua trọn bộ Đề thi Toán 9 Giữa/Cuối kì 1 và Giữa/Cuối kì 2 bản word có lời giải chi tiết:
- B1: gửi phí vào tk:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận đề thi
Đề thi Giữa kì 1 Toán 9
Hệ thống kiến thức Toán 9 Giữa học kì 1 năm 2024 (16 đề + ma trận)
Đề thi giữa kì 1 Toán 9 Trắc nghiệm + Tự luận năm 2024 (7 đề)
Đề thi Học kì 1 Toán 9
Đề thi Giữa kì 2 Toán 9
Đề thi Học kì 2 Toán 9
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 1
Năm học 2024 - 2025
Môn: Toán 9
Thời gian làm bài: phút
(Đề thi số 1)
Bài 1: (1,0 đ) : Tìm điều kiện của x để các căn thức sau có nghĩa.
![[Năm 2024] Đề thi Giữa kì 1 Toán 9 có đáp án (10 đề)](../de-thi-lop-9/images/de-thi-giua-ki-1-toan-lop-9-co-dap-an-2021-24855.png)
Bài 2 : (2,0 đ) Tính :
![[Năm 2024] Đề thi Giữa kì 1 Toán 9 có đáp án (10 đề)](../de-thi-lop-9/images/de-thi-giua-ki-1-toan-lop-9-co-dap-an-2021-24858.png)
Bài 3 : (1,0 đ) Cho biểu thức ![[Năm 2024] Đề thi Giữa kì 1 Toán 9 có đáp án (10 đề)](../de-thi-lop-9/images/de-thi-giua-ki-1-toan-lop-9-co-dap-an-2021-24859.png)
a)Rút gọn A.
b)Tìm x để A = 6
Bài 4 : (2,0 đ): Cho biểu thức ![[Năm 2024] Đề thi Giữa kì 1 Toán 9 có đáp án (10 đề)](../de-thi-lop-9/images/de-thi-giua-ki-1-toan-lop-9-co-dap-an-2021-24862.png)
a) Rút gọn biểu thức M
b) Tính giá trị của M khi ![[Năm 2024] Đề thi Giữa kì 1 Toán 9 có đáp án (10 đề)](../de-thi-lop-9/images/de-thi-giua-ki-1-toan-lop-9-co-dap-an-2021-24864.png)
c) Tìm giá trị của x để M > 0
Bài 5 (3,0 đ): Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn : BH = 4 cm và HC = 6 cm.
a) Tính độ dài các đoạn AH, AB, AC.
b) Gọi M là trung điểm của AC. Tính số đo góc AMB (làm tròn đến độ).
c) Kẻ AK vuông góc với BM (K thuộc BM). Chứng minh : BK.BM = BH.BC
Bài 6 (1,0đ): Giải phương trình sau.
![[Năm 2024] Đề thi Giữa kì 1 Toán 9 có đáp án (10 đề)](../de-thi-lop-9/images/de-thi-giua-ki-1-toan-lop-9-co-dap-an-2021-24865.png)
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1
Năm học 2024 - 2025
Môn: Toán 9
Thời gian làm bài: phút
(Đề thi số 1)
Bài 1: (1.5 điểm) Thực hiện các phép tính:
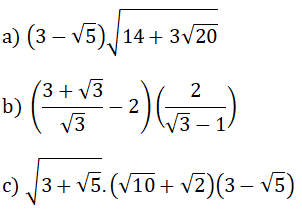
Bài 2: (1.5 điểm) Cho hàm số y = 2x + 3 có đồ thị (d1) và hàm số y = – x có đồ thị (d2).
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d1) và (d2) bằng phép toán.
Bài 3: (1.5 điểm) Cho biểu thức:
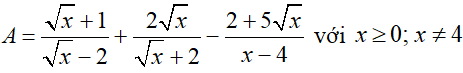
a) Thu gọn biểu thức A.
b) Tìm giá trị nhỏ nhất của A.
Bài 4: (2 điểm) Giải các phương trình:
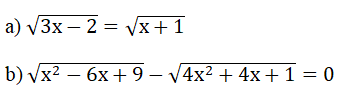
Bài 5: (3.5 điểm) Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.
a) Chứng minh H là trung điểm của AB và tam giác OMA đều.
b) Chứng minh tứ giác OAMB là hình thoi.
c) Tiếp tuyến tại A của (O) cắt tia OM tại C. Chứng minh CB = CA.
d) Đường thẳng vuông góc với OA tại O cắt BC tại N. Chứng minh MN là tiếp tuyến của đường tròn (O).
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa học kì 2
Năm học 2024 - 2025
Môn: Toán 9
Thời gian làm bài: phút
(Đề thi số 1)
Bài 1 (2 điểm) Giải các hệ phương trình sau:
a.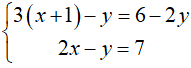 
b.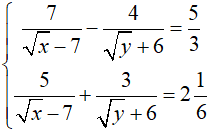 
Bài 2 (2 điểm) Gải bài toán bằng cách lập phương trình hoặc hệ phương trình’
Hai tổ sản xuất trong tháng thứ nhất làm được 1000 sản phẩm. Sang tháng thứ hai, do cải tiến kĩ thuật nên tổ một vượt mức 20%, tổ hai vượt mức 15% so với tháng thứ nhất. Vì vậy, cả hai tổ sản xuất được 1170 sản phẩm. Hỏi tháng thứ nhất, mỗi tổ sản xuất được bao nhiêu sản phẩm?
Bài 3 (2 điểm)
Cho đường thẳng (d) có phương trình y = ax + b. Tìm a, b biết (d) song song với đường thẳng (d’) có phương trình: y = -3x + 5 và đi qua điểm A thuộc Parabol (P) có phương trình y = x2 có hoành độ bằng – 2.
Bài 4 (3,5 điểm) Cho đường tròn (O; R), kẻ đường kính AB. Điểm M bất kì trên (O) sao cho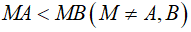 
. Từ M kẻ 
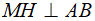tại H. Vẽ đường tròn (I) đường kính MH cắt MA, MB lần lượt tại E và F.
a. Chứng minh: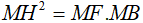 
và ba điểm E, I, F thẳng hàng.
b. Kẻ đường kính MD của đường tròn (O), MD cắt đường tròn (I) tại điểm thứ hai là N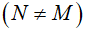 
. Chứng minh tứ giác BONF nội tiếp.
c. MD cắt EF tại K. Chứng minh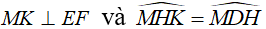 
d. Đường tròn (I) cắt đường tròn (O) tại điểm thứ hai là P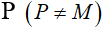 
. Chứng minh ba đường thẳng MP, FE và BA đồng quy.
Bài 5 (0,5 điểm) Cho các số không âm x, y, z thỏa mãn x + y + z = 1. Tìm giá trị lớn nhất của biểu thức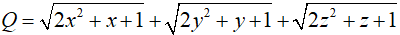 
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 2
Năm học 2024 - 2025
Môn: Toán 9
Thời gian làm bài: phút
(Đề thi số 1)
Câu 1: Cho hàm số y = -3x2. Kết luận nào sau đây là đúng :
A. Hàm số trên luôn đồng biến
B. Hàm số trên luôn nghịch biến
C. Hàm số trên đồng biến khi x > 0, nghịch biến khi x < 0
D. Hàm số trên đồng biến khi x < 0, nghịch biến khi x > 0
Câu 2: Cho phương trình bậc hai x2 – 2(m + 1) x + 4m = 0. Phương trình có nghiệm kép khi m bằng:
A. 1 C. Với mọi m
B. –1 D. Một kết quả khác
Câu 3: Cung AB của đường tròn (O; R) có số đo là 60o. Khi đó diện tích hình quạt AOB là:
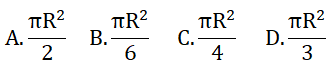
Câu 4: Tứ giác MNPQ nội tiếp đường tròn khi:
A.∠(MNP) + ∠(NPQ) = 180o
B.∠(MNP) = ∠(MPQ)
C. MNPQ là hình thang cân
D. MNPQ là hình thoi
Phần tự luận (8 điểm)
Bài 1 (2,0 điểm)
1) Tìm điều kiện xác định của biểu thức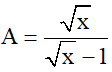 
2) Cho biểu thức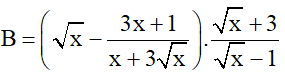 
với x > 0; x ≠ 1
a) Rút gọn biểu thức B
b) Tìm giá trị nhỏ nhất của P = A.B với x > 1
Bài 2 (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một tấm bìa hình chữ nhật có chiều dài hơn chiều rộng 3dm. Nếu giảm chiều rộng đi 1dm và tăng chiều dài thêm 1dm thì diện tích tấm bìa là 66 Tính chiều rộng và chiều dài của tấm bìa lúc ban đầu.
Bài 3 (2,0 điểm)
1) Cho phương trình x4 + mx2 - m - 1 = 0(m là tham số)
a) Giải phương trình khi m = 2
b) Tìm giá trị của m để phương trình có 4 nghiệm phân biệt.
2) Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x2 và đường thẳng (d): y = 2x + m (m là tham số).
a) Xác định m để đường thẳng (d) tiếp xúc với parabol (P). Tìm hoành độ tiếp điểm.
b) Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm A, B nằm về hai phía của trục tung, sao cho diện tích có diện tích gấp hai lần diện tích (M là giao điểm của đường thẳng d với trục tung).
Bài 4 (3,5 điểm) Cho đường tròn (O; R), dây AB. Trên cung lớn AB lấy điểm C sao cho A < CB. Các đường cao AE và BF của tam giác ABC cắt nhau tại I.
a) Chứng minh tứ giác AFEB là tứ giác nội tiếp
b) Chứng minh CF.CB = CE.CA
c) Nếu dây AB có độ dài bằng R√3 , hãy tính số đo của (ACB)
d) Đường tròn ngoại tiếp tam giác CEF cắt đường tròn (O; R) tại điểm thứ hai là K (K khác C). Vẽ đường kính CD của (O; R). Gọi P là trung điểm của AB. Chứng minh rằng ba điểm K, P, D thẳng hàng.
