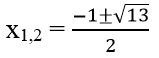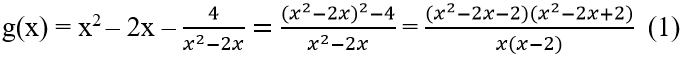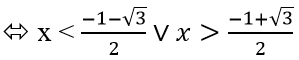Bằng cách sử dụng hằng đẳng thức a2 – b2 = (a – b)(a + b) hãy xét dấu

Ôn tập chương 4 (Bài tập trắc nghiệm)

Bài 11 trang 107 Toán 10: a) Bằng cách sử dụng hằng đẳng thức a2 – b2 = (a – b)(a + b) hãy xét dấu

f(x) = x⁴ – x² + 6x – 9 và g(x) = x² - 2x – 4/(x²-2x )

b) Hãy tìm nghiệm nguyên của bất phương trình sau:

x(x³ – x +6) > 9

Trả lời

Xét dấu của f(x) = x⁴ – x² + 6x – 9 = x⁴ – (x² - 6x + 9) = (x² – x +3)( x² + x – 3) (1)

Mà x² – x + 3 có Δ < 0 nên x² – x +3 > 0, ∀x nên (1) ⇔ f(x) có dấu của x² + x – 3

Vì x² + x – 3 có Δ = 13 nên x² + x – 3 có hai nghiệm

Vậy, f(x) > 0 khi x < (-1-√13)/2 hay x > (-1+√13)/2

f(x) < 0 khi (-1-√13)/2 < x < (-1+√13)/2

f(x) = 0 khi x = (-1-√13)/2 ∨ x = (-1+√13)/2

Xét dấu của

Mà x² – 2x + 2 > 0,∀x ∈R nên (1) cho g(x) có dấu của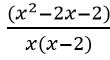

Bảng xét dấu

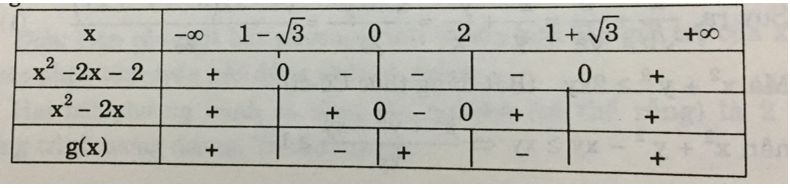
vậy, g(x) > 0 khi x ∈ (-∞;1-√3)∨(0;2)∨(1+√3;+∞)

g(x) < 0 khi 1-√3 < x < 0 ∨ (2;1+√3)

b) x(x³ – x + 6) > 9 ⇔ x⁴ – x² + 6x – 9 > 0

Mà √13<3 và x nguyên nên ta chọn: x ≤-3 hay x ≥ 2

Vậy nghiệm nguyên của x(x³ – x + 6) > 9 là {x ∈ Z/ x ≤ -3∨x≥2}