Cho a > 0, b > 0. Chứng minh rằng: a/√b + b/√a ≥ √a + √b

Ôn tập chương 4 (Bài tập trắc nghiệm)

Bài 10 trang 107 Toán 10: Cho a > 0, b > 0. Chứng minh rằng: a/√b + b/√a ≥ √a + √b

Trả lời

Cách 1: Sử dụng các phép biến đổi tương đương để chứng minh bất đẳng thức.

Ta có:

Do đó: 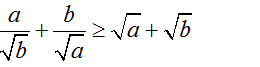(đpcm)

Cách 2: Áp dụng bất đẳng thức Cauchy cho hai số dương $\frac{a}{\sqrt{b}}$ và $\sqrt{b}$ ta có:

$\frac{a}{\sqrt{b}}+\sqrt{b}\ge 2\cdot \sqrt{\frac{a}{\sqrt{b}}\cdot \sqrt{b}}=2\sqrt{a}$ (1)

Tương tự ta có:

$\frac{b}{\sqrt{a}}+\sqrt{a}\ge 2\cdot \sqrt{\frac{b}{\sqrt{a}}\cdot \sqrt{a}}=2\cdot \sqrt{b}$ (2)

Cộng vế với vế của (1) và (2) ta được:

$\frac{a}{\sqrt{b}}+\sqrt{b}+\frac{b}{\sqrt{a}}+\sqrt{a}\ge 2\sqrt{a}+2\sqrt{b}$

⇔ $\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{a}}\ge \sqrt{a}+\sqrt{b}$ (điều phải chứng minh)

Dấu bằng xảy ra khi và chỉ khi a = b > 0.